A1.1 Termalizzazione. Radiazione di corpo nero. Emissività stellare.
Come mostrato da Max Planck, la radiazione elettromagnetica deve essere
considerata come composta da unità elementari (quanti di energia,
o fotoni) ad ognuno dei quali risulta associata una energia E =
, dove:
- h = costante di Plank =
erg
= frequenza della radiazione (cicli/sec)
Un campo di radiazione elettromagnetica (quale è la luce) può
quindi essere visto come un gas di fotoni tra loro non interagenti.
In presenza di materia a temperatura T, i fotoni interagiscono però
con le particelle attraverso tutta una serie di processi che conducono i fotoni verso una
situazione energetica di equilibrio, retta dalla legge di distribuzione di Plank
[1]
ove è la densità di energia della radiazione
con frequenza tra
, k la costante di Boltzmann
Nel suo aspetto più generale la distribuzione di Plank è una
conseguenza delle necessità che discendono dalla meccanica statistica. Un gas di particelle, se le particelle possono
scambiarsi energia tramite mutue interazioni, deve evolvere verso
una situazione di equilibrio nella quale la velocità delle
particelle è retta dalla nota formula di Maxwell-Boltzmann (fig.
1.12): in queste condizioni si può parlare di
equilibrio termico e definire una temperatura T del gas così
termalizzato.
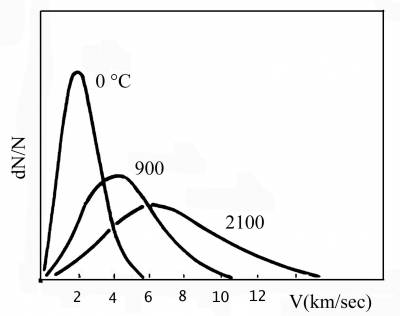
Fig. 1.12 La distribuzione Maxwelliana delle velocità U
delle particelle di un gas segue la legge
<tex>
$ {dN/N} = 4 \pi
\left({m\over 2 \pi k T}\right)^{3/2} \exp{\left(-m U^2 \over 2 k
T \right)} U^2 dU $
</tex>,
dove dN è il numero di particelle
nell'intervallo di velocità dU, m è la massa delle particelle e T la temperatura del gas.
Analogamente, una radiazione elettromagnetica che possa interagire
con un sistema di particelle termalizzato evolve verso la
situazione di equilibrio descritta dalla legge di Plank. In tutti e
due i casi, il raggiungimento della termalizzazione della materia
e della radiazione sarà tanto più rapido quanto più
efficienti sono i meccanismi di interazione e scambio energetico
materia-materia e materia-radiazione.
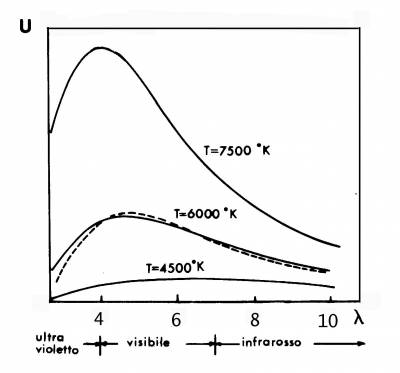
Fig. 1.13 L'emissività di un corpo nero per varie temperature in funzione della lunghezza d'onda (in 103 Angstrom). La curva a tratti riporta schematicamente l'andamento dello spettro solare.
Si può mostrare che l'energia S irradiata in un secondo nell'
angolo solido dalla unità di superficie di un corpo in
equilibrio termodinamico (corpo nero) risulta
[2]
e quindi, indicando con l'energia irraggiata
nell'intervallo di frequenza
e
[3]
dove è nota come funzione di Plank.
Poichè per la lunghezza d'onda è
si ha
e
, il flusso
energetico per unità di superficie e di lunghezza d'onda (
emittanza) risulta (fig. 1.13)
[4]
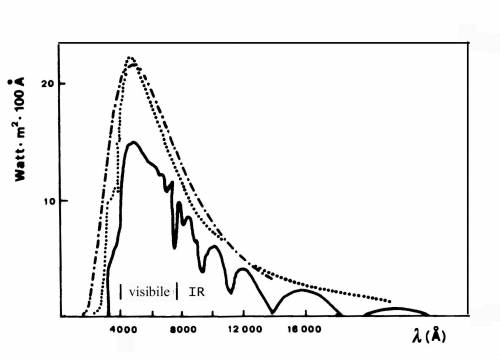
Fig 1.14 Spettro del Sole al di fuori dell'atmosfera (punti) confrontato con il corpo neroa 6000 K (tratto e punto) e con lo spettro
della radiazione raccolta alla superficie della Terra. Si notino in questo ultimo spettro, al di là di 8000 A, le bande degli assorbimenti
causati da ,
,
e
Per l'energia irraggiata per unità di superficie e di tempo da un corpo nero si ha
(legge di Stefan-Boltzman)
con
Annullando nella (4) la derivata si
ottiene per la lunghezza d'onda cui corrisponde il massimo di
emissione
L'emissione delle superfici stellari approssima in generale
distribuzioni (spettri) di corpo nero. In tal senso si può
parlare di temperatura della radiazione e delle superfici
stellari. La fig. 1.14 pone ad esempio a confronto lo
spettro della radiazione solare con la distribuzione di corpo
nero, mostrando come alla superficie del Sole debba essere
attribuita una temperatura che si aggira attorno a
Di particolare importanza per le stelle è la temperatura efficace
, definita dalla legge di Stefan-Boltzmann
dove L e R indicano rispettivamente luminosità e raggio della stella. La temperatura efficace è dunque la temperatura che avrebbe la superficie della stella se emettesse esattamente come un corpo nero.
