A2.1 Energia interna, pressione della radiazione e pressione del gas perfetto
Si è già indicato ($ \rightarrow A1.1$) come all'interno di una struttura stellare materia e radiazione siano ambedue da considerarsi termalizzate alla temperatura locale T. In tali condizioni la densità e la distribuzione in frequenza dei fotoni restano regolate dalle leggi del corpo nero, la densità di energia risultando in particolare pari a $U = a T^4$. In tali condizioni è anche facile ricavare il valore della pressione di radiazione, collegata - come nel caso delle particelle- al momento trasportato dai fotoni.
Immaginiamo la radiazione intrappolata all'interno di un
cubetto di volume unitario a superfici interne perfettamente
riflettenti. Un generico fotone di energia $E=h\nu$ e momento
$p=h\nu/c$ avrà una direzione di moto definita dai tre coseni direttori
$$\frac {c_x}{c}, \frac {c_y}{c}, \frac {c_z}{c}$$
degli angoli formati dal vettore velocità $\overline c$
con i tre assi delle coordinate. Nell'unità di tempo si
avranno cx urti contro le due pareti perpendicolari all'asse x
(Figura 2.6) ed in ogni urto verrà scambiata una
quantità di moto pari in modulo a $2(h\nu/c) c_x/c$. La somma
(in modulo) dei momenti scambiati dal fotone con le 6 pareti del
cubetto nell'unità di tempo risulta
$$2\frac {h\nu}{c} \frac {c_x}{c}+ 2\frac {h\nu}{c}\frac {c_y}{c}+ 2\frac {h\nu}{c} \frac {c_z}{c} = 2 \frac {h\nu}{c^2}(c_x^2+ c_y^2+ c_z^2) = 2 h\nu = 2E$$
Se ne conclude che il gas di fotoni isotropi scambia
nell'unità di tempo con ognuna delle pareti del cubetto una
quantità di moto pari a
$$\Delta p = E/3$$
dove E è la somma delle energie dei singoli fotoni.
Poiché $\Delta p=F\Delta t$ si ricava che il gas di fotoni opera
sulla superficie unitaria una forza (la pressione) pari a
$$P_r = E/3$$
Per una distribuzione di corpo nero si ricava cos\`i il
valore della pressione di radiazione
$$P_r = \frac {1}{3} U = \frac {a}{3} T^4$$
Con considerazioni del tutto analoghe si ricava per un gas perfetto
non relativistico
$$P_g = \frac {1}{3} \Sigma m_iv_i^2 = \frac {2}{3} W$$
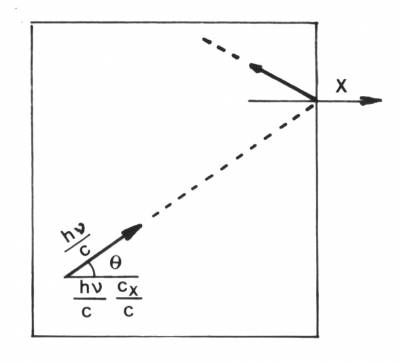
Figura 2.6 Nell'urto elastico contro la parete un
fotone di impulso <tex>h$\nu$/c</tex> inverte la componente x cedendo un
impulso pari a
$$\frac{2 h \nu}{c}{cos \theta} = \frac{2 h \nu}{c} {\frac{c_x}{c}}$$
dove $W=\Sigma \frac {1}{2} m_iv_i^2$
rappresenta la densità di energia cinetica. Poiché l'energia cinetica media
per molecola è pari a
$3/2 kT, \Sigma\frac{1}{2} m_i v_i^2 = nkT$ dove n rappresenta il numero di particelle per
unità di volume. Si ritrova così l'equazione di stato del gas
perfetto
$$P_g = nkT$$
Per un gas perfetto monoatomico $W=U=3/2 kT$. Nel caso più
generale $U=N/2 kT$, dove N è il numero di gradi di libertà
delle particelle, e si ricava facilmente
$$P_g = \frac {2}{N} U$$
che, in analogia di quanto già visto per la
radiazione, pone in relazione la pressione con l'energia interna
per unità di volume.
