Astrofisica Stellare

La diffusa evidenza del fenomeno “stella” testimonia che la formazione di stelle costituisce una processo spontaneo e naturale nell'evoluzione della materia nell'Universo. Ed in effetti il Sole, come tutte le altre stelle, indubbiamente altro non è che il prodotto di una aggregazione spontanea di materia diffusa sotto l'influenza della gravitazione. La storia dell'evoluzione di una stella sarà dunque la storia della contrazione di una massa di gas sotto l'influenza del proprio campo gravitazionale (struttura autogravitante). Per affrontare un tale argomento conviene esaminare con qualche dettaglio la struttura di tali oggetti, al fine di comprenderne e di prevederne le principali caratteristiche. Ciò può essere fatto investigando in forma quantitativa le problematiche che vengono suggerite da pur semplici evidenze osservative.

La prima di queste evidenze è che il Sole mantiene ed ha mantenuto per un lunghissimo tempo le sue dimensioni. La materia che costituisce il Sole, pur soggetta ad una intensa forza gravitazionale, non mostra di muoversi verso il centro di gravità con tempi scala meccanici, cioè con i tempi tipici dei moti che si sviluppano sotto l'azione della forza gravitazionale. Per fissare le idee, possiamo valutare che alla superficie del nostro Sole, essendo massa e raggio del Sole , si ha una accelerazione di gravità

circa 30 volte superiore che alla superficie della Terra. Poichè in un moto uniformemente accelerato , un corpo alla superficie del Sole sul quale agisse liberamente la gravità percorrerebbe uno spazio pari al raggio del Sole in un tempo

.

Si ricava così un ordine di grandezza dei tempi caratteristici sui quali opererebbe la gravità su scala solare. I secondi ricavati assicurano che se la forza di gravità fosse libera di operare, il Sole dovrebbe rapidamente modificarsi sotto i nostri occhi. Poichè ciò non avviene, dobbiamo concludere che la forza di gravità è contrastata ed annullata dalle forze di pressione generate nel gas, producendo una struttura che definiremo quasi stazionaria, perchè - come constateremo - pur se le forze di pressione annullano le forze di gravità la struttura è costretta sia pur lentamente ad evolvere.

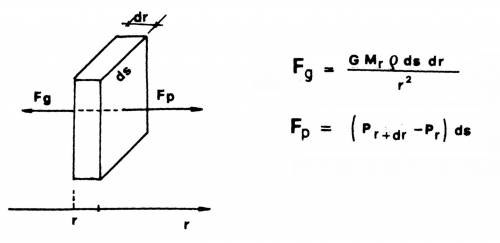
Figura 2.1 Il bilancio della forza di gravità F_g e delle forze di pressione F_p per un generico elemento di materia di volume dV = dS dr.

E' facile tradurre le precedenti considerazioni in una relazione quantitativa. Assumendo la simmetria sferica della struttura solare - come suggerito dall'evidenza osservativa - il bilancio tra le forze di pressione e quelle gravitazionali (fig. 2.1) per un generico elemento di massa fornisce la relazione dell' equilibrio idrostatico

[1]

dove P rappresenta la pressione totale operante nell'ambiente (quindi non la sola pressione del gas A2.1), la densità locale ed M_r la massa contenuta all'interno del generico raggio r.

Questa equazione fornisce una prima relazione tra le tre grandezze incognite P, ed M_r , assicurando che la pressione deve crescere con continuità muovendosi verso l'interno della stella. In realtà una delle incognite è solo formale, perchè dalla definizione di M_r si ricava subito l' equazione di continuità

[2]

Aggiunta alla precedente, l'equazione di continuità forma un sistema di due equazioni differenziali nelle tre indicate incognite. Dalla sola condizione di equilibrio non è dunque possibile definire l'andamento delle variabili fisiche lungo la struttura, e ciò non sorprende perchè la struttura medesima dipenderà da come e P sono tra loro collegate, cioè dall'equazione di stato che per ogni assegnata composizione della materia consisterà in una relazione del tipo

[3]

E' subito visto che l'introduzione dell'equazione di stato, se aumenta il numero delle equazioni aumenta anche il numero delle incognite, introducendo la nuova incognita “temperatura” . Come peraltro prevedibile, la distribuzione delle temperature è quindi un ingrediente essenziale nel determinare lo stato della struttura. Sarà di conseguenza necessario, in linea del tutto generale, ricorrere ad opportune valutazioni delle leggi fisiche che regolano la distribuzione delle temperature nella materia stellare, determinando l'andamento del gradiente di temperatura dT/dr.

Notiamo che la presenza di un gradiente di temperatura implica la conseguente presenza di un flusso di energia che tende a riequilibrare lo stato energetico dei diversi strati di materia. Le interazioni particella-particella e fotone-particella tendono inevitabilmente a ridistribuire l'energia, producendo un trasporto di calore verso le zone a minor temperatura. E' peraltro noto come i possibili meccanismi per tale trasporto siano conduzione, convezione ed irraggiamento. Escludendo per il momento il caso della convezione, negli altri due casi si ha - come regola generale - che il flusso di calore è proporzionale al gradiente

[4]

relazione che può essere letta come una delle tanti leggi di proporzionalità tra causa (dT/dr) ed effetto (il flusso ), una sorta di legge di Ohm dove la costante rappresenta la “resistenza” al trasporto. La materia all'interno di una stella si trova in generale nello stato gassoso, cui corrisponde (ma con importanti eccezioni) una trascurabile efficienza dei meccanismo conduttivi. In tal caso si può dimostrare ( A2.2) che tra il flusso trasportato per radiazione (dai fotoni) ed il gradiente di temperatura intercorre la relazione

[5]

dove a = costante del corpo nero = 7.6 10^-15 cm, c= velocità della luce e opacità per grammo di materia è definita dalla relazione

con cammino libero medio dei fotoni: minore il cammino libero medio maggiore l'opacità.

Da tale equazione del trasporto radiativo si ricava non solo che un gradiente di temperatura genera un flusso, ma anche che la presenza di un flusso implica un gradiente di temperatura. L'emergere di un flusso luminoso dalle strutture stellari è quindi indicazione che la temperatura cresce dalla superficie verso l'interno, e che tale aumento deve continuare sinché la struttura è percorsa da un flusso di energia uscente. Se ne trae anche la conseguenza che se nelle zone centrali di una struttura stellare non vi sono sorgenti (positive o negative) di energia, allora tali zone devono tendere ad una situazione isoterma. Un gradiente di temperatura produrrebbe infatti un flusso volto a riequilibrare le differenze di temperatura.

Nell'equazione del trasporto il flusso locale può utilmente essere espresso, per ogni r, in termini della flusso energetico totale attraverso la superficie sferica di raggio r ()

talchè l'equazione del trasporto diventa, nel caso di trasporto radiativo

[6]

Abbiamo così una quarta relazione, che introduce l'ulteriore incognita L_r , così che in totale si hanno quattro equazioni che contengono le sei variabili r, L _r , P, T, M _r , . La condizione su L _r è peraltro subito fornita dalla conservazione dell'energia

[7]

dove rappresenta la produzione di energia per grammo di materia e per secondo. La relazione precedente rappresenta il bilancio energetico, stabilendo che se l'energia totale che fluisce attraverso la struttura subisce una variazione tra r e r+dr ciò e' dovuto alla produzione o assorbimento di energia nella corrispondente massa . E' proprio questa diretta collegabilità al bilancio energetico che fa preferire l'uso della variabile L _r nell'equazione del trasporto.

Con questa ultima relazione si raggiunge un sistema di cinque equazioni (di cui quattro differenziali) che legano i sei parametri

1. equilibrio idrostatico
2. equazione di continuità
3. equazione del trasporto
4. conservazione dell'energia
5. equazione di stato

sistema che, con le opportune condizioni al contorno, può essere risolto, ricavando l'andamento di cinque delle precedenti variabili in funzione dell'andamento della sesta variabile assunta come variabile indipendente.

Ripercorrendo le assunzioni operate concludiamo che il sistema di equazioni governa ogni sistema a simmetria sferica, autogravitante, in equilibrio idrostatico e sinchè si resti nel campo di applicabilità della meccanica non relativistica (A2.3). Al variare della composizione chimica della materia stellare, le soluzioni si differenzieranno non per l'algoritmo delle equazioni fisico matematiche sin qui descritte, ma per il diverso comportamento fisico della materia ``depositato'' in tali equazioni dalle tre relazioni

1. equazione di stato
2. opacità della materia stellare
3. produzione di energia

ove si è esplicitamente indicato come ci si attenda che non solo la pressione ma anche l'opacità e la produzione di energia dipendano dalle condizioni termodinamiche della materia oltre che dalla non esplicitata composizione chimica della materia medesima.