Indice
2.6 Metodi di calcolo
L'andamento delle variabili fisiche all'interno di una struttura stellare è dunque retto da un sistema di quattro equazioni differenziali che, integrato con l'equazione di stato, consente di ricavare l'andamento di cinque delle variabili in funzione di una sesta assunta come variabile indipendente per ogni prefissato valore della massa M della struttura e per ogni prefissata distribuzione della composizione della materia all' interno della struttura medesima. Notiamo subito che l'esistenza di quattro equazioni differenziali del primo ordine richiederà l'individuazione di quattro opportune condizioni al contorno. Stante la complessità del sistema non esistono in generale soluzioni analitiche e la soluzione è ottenuta sulla base di tecniche di calcolo numeriche basate su metodi a differenze finite, ove cioè i differenziali sono approssimati con incrementi piccoli ma finiti, così che le relazioni differenziali vengono trasformate in equazioni algebriche.
Prima di illustrare i due diversi metodi in uso per la soluzione di tali equazioni discuteremo l'integrazione degli strati atmosferici, in quanto ingrediente di base che entra nell'architettura di tutti e due i metodi cui abbiamo fatto riferimento.
2.6.1 Integrazione degli strati atmosferici
Ricordiamo che per gli strati atmosferici abbiamo stabilito la
relazione differenziale (2.15) che, in termini di differenze
finite può essere scritta come
$$ [19] \ \ P_{j+1} - P_j = \frac {g}{\overline \kappa} (\tau_{j+1} -\tau_j)$$
ove, in accordo con il metodo delle differenze finite,
l'intervallo di integrazione è stato
opportunamente suddiviso prefissando N valori
della
variabile indipendente (N mesh) per j che va da 1 a N.
è il valore, da determinare, della variabile nel generico punto
“j”. Accanto a questa relazione differenziale abbiamo le due
ulteriori relazioni, qui ripetute per comodità
T = T ( $\tau$, T$_e$ )
P = P ( $\rho$, T )
Tali relazioni consentono di ricavare l'andamento delle variabili
in un atmosfera stellare per ogni prefissato valore
della massa stellare M, quando siano assegnati due tra i tre
parametri
il terzo restando determinato dalla
relazione
. Assegnando ad esempio,
come d'uso,
ed
restano fissati
e
.
Sotto tali condizioni, note le grandezze nel generico punto j la
(19) fornisce il valore della pressione nel punto j+1
$$P_{j+1}= P_j + \frac {g}{\kappa} ( \tau_{j+1} - \tau_j)$$
la temperatura nello stesso punto j+1 è fornita dalla
$T(\tau, T_e)$, dall'equazione di stato si ricava allora la
densità e, con essa, il valore di .
Basta quindi fornire i valori per
per ricavare per
ricorrenza l'andamento di
su tutto l'intervallo considerato.
Tale integrazione per tangenti (cfr. fig.2.5) risulterà
tanto più accurata quanto più piccoli gli intervalli
(passi) della variabile indipendente. Nella pratica, tali passi
possono essere collegati alla condizione che la variabile
dipendente lungo un passo non vari più di una prefissata
percentuale, e la bontà dell'integrazione può essere
controllata verificando, ad esempio, che un ulteriore dimezzamento
dei passi non vari il risultato entro la richiesta precisione.
Sulla base di tale schema sono costruiti algoritmi di calcolo
numerico (ad es. il metodo di Runge-Kutta) che, con l'introduzione
di opportuni coefficienti di correzione basati sull'andamento della
funzione già integrata consentono di minimizzare il numero di
passi per ogni prefissata precisione.
2.6.2 Il metodo del fitting
Per ogni prefissato valore della massa totale M e per ogni scelta
dei due parametri L e Te si possono quindi ricavare i valori di
P e T (e quindi ) alla base dell'atmosfera, ove sono quindi
disponibili i valori di tutte e sei le variabili
$$r=R, L_r=L, P, T, \rho, M_r=M$$
che compaiono nel sistema di equazioni per l'equilibrio stellare.
Supponendo di utilizzare subito come variabile indipendente Mr,
possiamo riscrivere le equazioni di equilibrio in funzioni
della variazioni di tale variabile. Ponendo e
passando nuovamente allo schema di differenze finite si ottiene
[21]
[22]
[23]
se , altrimenti
[24]
[25]
Analogamente a quanto già discusso per l'integrazione
atmosferica, se nel mesh sono noti i valori delle
variabili r, L _r , P, T,$\rho$ (dall'equazione di stato),
$\overline \kappa (\rho, T)$ e $\varepsilon (\rho, T)$ sono noti i
valori di tutti i coefficienti a secondo membro delle relazioni
precedenti, e per ogni assunto $\Delta M_r = M_{r,j+1} -
M_{r,j}$ le relazioni forniscono il valore delle variabili nel
mesh j+1. Partendo dal primo mesh, alla base dell'atmosfera,
l'iterazione di tale procedura consente di spingere l'integrazione
lungo tutta la struttura.
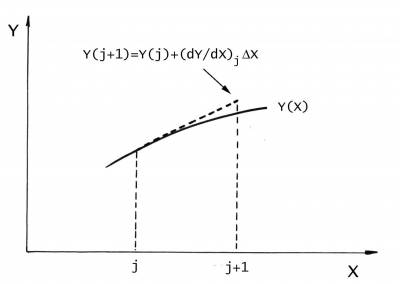
Figura 2.5 Nell'integrazione per tangenti, noto il valore
della derivata della generica variabile Y(X) nel mesh Xj,
si pone Yj+1=(dY/dX)j(Xj+1-Xj),
valutando così la variazione lungo la tangente definita dalla derivata
in Xj, con un errore che diminuisce al diminuire dell'assunto
.
Perchè il risultato possa rappresentare una stella occorre e
basta che per $M_r = 0$ (centro della struttura) risulti r = 0 e
$L _r = 0$. In linea di principio si potrebbe pensare di
identificare la soluzione variando opportunamente i valori di L e
Te di partenza, sino a soddisfare le citate condizioni
centrali. Nella pratica ciò non è consentito dalla eccessiva
sensibilità delle soluzioni a $M _r = 0$ dalle condizioni
superficiali. Il metodo del “fitting” (cioè del raccordo) supera
questa difficoltà procedendo ad una integrazione dall' esterno a
partire una coppia di valori di prova L e T _e , spingendo
l'integrazione sino ad un prefissato valore della massa M _r =
M _F (massa di fitting) ottenendo in tale punto una
quadrupletta di valori $r ^e , L _r^e , P ^e , T ^e$, ove l'indice
“e” sta ad indicare che tali valori sono il risultato
dell'integrazione esterna.
$$L, T _e \Rightarrow r^e (L, T _e ), L ^e (L, T _e ), P ^e (L, T _e ), T ^e (L, T _e )$$
ove si è evidenziata la ovvia dipendenza dei valori della
quadrupletta dai due assunti valori di prova L e Te . Si procede
poi ad una integrazione dal centro imponendo in tale punto
$r = L _r = 0$ e assumendo due valori di prova Pc e Tc ricavando
nello stesso punto di fitting un'altra quadrupletta di valori
$r ^i , L _r^i , P ^i , T ^i$ ,
$$P _c , T _c \Rightarrow r^i (P _c , T _c ), L _r^i (P _c , T _c ), P ^i (P _c , T _c ), T ^i (P _c , T _c )$$
e l'integrazione sarà corretta solo quando le due quadruplette
vengano a coincidere.
In generale, le integrazioni basate sui parametri di
prova forniranno al fitting valori non concordanti, e porremo per tali discrepanze
$$r^e -r^i = \varepsilon _r$$
$$L_r^e -L_r^i = \varepsilon _L$$
$$P^e -P^i = \varepsilon _P$$
$$T^e -T^i = \varepsilon _T$$
Tenuto presente che i valori delle due quadruplette dipenderanno dai valori di prova assunti, rispettivamente, per $L, T_e$ e $P_c , T_c$, il metodo del fitting consiste nel valutare quali le variazioni da apportare ai quattro valori di prova per annullare le discrepanze tra le due quadruplette, o - nella pratica - perchè le discrepanze $(P^i - P^e )/P^i$ e simili scendano al di sotto di una soglia di precisione tipicamente non maggiore di 10-4.
In approssimazione lineare, la variazione dei valori delle quadruplette può essere espressa in funzione delle derivate parziali dei valori medesimi rispetto ai relativi valori di prova. Così, ad esempio
$$\Delta P^e = (\partial P^e / \partial L)_{Te=cost} \Delta L + (\partial P^e / \partial T_e)_ {L=cost} \Delta T_e$$
e, corrispondentemente,
$$\Delta P^i = (\partial P^i / \partial P_c)_ {Tc=cost} \Delta P_c + (\partial P^i / \partial T_c)_{P_c=cost} \Delta T_c$$
Sulla base di simili relazioni, per la variazione delle discrepanze si ottiene
[26]
$$\Delta (r^e - r^i) =
(\frac{\partial r^e}{\partial L})_{T_e} \Delta L +
(\frac{\partial r^e}{\partial T_e})_L \Delta T_e +
(\frac{\partial r^i}{\partial P_c})_{T_c} \Delta P_c +
(\frac{\partial r^i}{\partial T_c})_{P_c} \Delta T_c$$
[27]
$$\Delta (L_r^e -L_ r^i) =
(\frac{\partial L_r^e}{\partial L})_{T_e} \Delta L +
(\frac{\partial L_r^e}{\partial T_e})_L \Delta T_e +
(\frac{\partial L_r^i}{\partial P_c})_{T_c} \Delta P_c +
(\frac{\partial L_r^i}{\partial T_c})_{P_c} \Delta T_c$$
[28]
$$\Delta (P^e - P^i) =
(\frac{\partial P^e}{\partial L})_{T_e} \Delta L +
(\frac{\partial P^e}{\partial T_e})_L \Delta T_e +
(\frac{\partial P^i}{\partial P_c})_{T_c} \Delta P_c +
(\frac{\partial P^i}{\partial T_c})_{P_c} \Delta T_c$$
[29]
$$\Delta (T^e - T^i) =
(\frac{\partial T^e}{\partial L})_{T_e} \Delta L +
(\frac{\partial T^e}{\partial T_e})_L \Delta T_e +
(\frac{\partial T^i}{\partial P_c})_{T_c} \Delta P_c +
(\frac{\partial T^i}{\partial T_c})_ {P_c} \Delta T_c$$
Imponendo che tali variazioni siano eguali ma di segno contrario
alle discrepanze $\varepsilon_i (i = 1, 4)$, così da annullare
le differenze delle due quadruplette al fitting, ove siano noti i
valori delle derivate si ottiene un sistema lineare di quattro
equazioni nelle quattro incognite $\Delta L$ , $\Delta T_e$ .
$\Delta P_c$, $\Delta T_c$ e con termini noti $ - \varepsilon_i
(i=1,4).$
I valori delle derivate parziali sono ricavati eseguendo quattro integrazioni,
due dall' esterno e due dall'interno, a partire dai valori al contorno
$$L + \delta L , T_e$$
$$L, T _e + \delta T_e$$
$$P_c , T _c + \delta T_c$$
$$P_c + \delta P_c , T_c$$
e ponendo per la generica variabile $X ^i_j (j=1, 4), X^e_j (j=1,4)$
[30]
$$\frac{\partial X^e_j}{\partial L} \approx \frac{X^e_j(L + \delta L, T_e) - X^e_j(L, T_e)}{\delta L}$$
e simili per le derivate rispetto alle altre tre condizioni al
contorno. La soluzione del sistema di quattro equazioni lineari
fornisce le quattro correzioni alle condizioni al contorno sulla
base delle quali operare una nuova coppia di integrazione
esterno-interno. Poichè la linearità del sistema delle
correzioni e' solo una approssimazione al primo ordine, la
soluzione viene in genere raggiunta attraverso una serie di
iterazioni, sempre che le iniziali condizioni al contorno non
siano troppo distanti da quelle finali, risultando all'interno di
quella che viene definita l' area di convergenza.
2.6.3 Il metodo di Henyey
Un approccio alternativo alla soluzione del problema consiste nel adottare una soluzione di prova, cioè assegnare in ogni punto un valore delle funzioni $(M$_r$), L$_r$(M$_r$), P(M$_r$), T(M$_r$)$, ed applicare un metodo che consente di correggere tali valori.
Possiamo riscrivere le equazioni dell'equilibrio sotto forma di
differenze finite e portando tutti i termini a primo membro,
ottenendo - ponendoci ad esempio nel caso di equilibrio radiativo - le
quattro relazioni algebriche
$$(P_{j+1} - P_j) / (r_{j+1} - r_j) - G M_{r,j} \rho_j / r_j^2 = 0$$
$$(M_{r,j+1} - M_{r,j}) / (r_{j+1}- r_j) - 4 \pi r_j^2 \rho = 0$$
$$(T_{j+1} - T_j) / (r_{j+1}- r_j) - (3/4ac) (\overline \kappa \rho_j / T_j^3) L_{r,j} / 4\pi r_j^2 = 0$$
$$(L_{r,j+1} - L_{r,j}) / (r_{j+1}- r_j) - 4 \pi r_j^2 \varepsilon = 0$$
Poiché la soluzione di prova non soddisfa le equazioni di equilibrio, le quattro eguaglianze a zero non saranno verificate, ed ognuna delle quattro relazioni darà, per ogni coppia degli N mesh, una discrepanza
$$\delta_{i,j} \ \ ( i=1,4 ; j=1, N-1)$$
Occorre dunque operare sui valori di prova assegnati negli N singoli mesh in cui è stata divisa la struttura al fine di azzerare i 4N-4 $\delta_{i,j}$ così che le relazioni di equilibrio risultino soddisfatte lungo tutta la struttura.
Notiamo al proposito che, avendo scelto come variabile indipendente <tex>M$_r$</tex> ed avendo dunque prefissato il valore di M$_r$ in opportuni mesh spaziati lungo la struttura, il generico $\delta_{i,j}$ resta una funzione algebrica dei valori delle quattro variabili nei mesh j e j+1
$$\delta_{i,j} = f(r_j, L_{r,j}, P_j, T_j, r_{j+1}, L_{r,j+1}, P_{j+1}, T_{j+1} )$$
di cui è possibile ricavare algebricamente i valori delle derivate parziali rispetto alle otto variabili.
Per la dipendenza del generico $\delta_{i,j}$ dalle funzioni di prova potremo dunque scrivere per ogni coppia di mesh e per ognuna delle 4 equazioni dell'equilibrio una relazione che lega le discrepanze al valore variabili
$$\Delta \delta_{i,j} = \frac {\partial \delta_{i,j}}{\partial r_j} \Delta r_j
+ \frac {\partial \delta_{i,j}}{\partial L_{r,j}} \Delta L_{r,j} +
\frac {\partial \delta_{i,j}}{\partial P_j} \Delta {P_j} +
\frac {\partial \delta_{i,j}}{\partial T_j} \Delta {T_j} +
\frac {\partial \delta_{i,j}}{\partial r_{j+1}} \Delta r_{j+1} + $$
$$ + \frac {\partial \delta_{i,j}} {\partial L_{r,j+1}} \Delta L_{r,j+1} +
\frac {\partial \delta_{i,j}}{\partial P_{j+1}} \Delta P_{j+1}+
\frac {\partial \delta_{i,j}} {\partial r_{j+1}} \Delta T_{j+1}$$
imponendo che per ogni coppia e per ogni equazione $\delta{i,j}$ subisca
una variazione eguale e di segno contrario alla discrepanza trovata, si
ottiene in definitiva un sistema di 4N-4 equazioni nelle 4N incognite
$$\Delta {r_j}, \Delta L{r,j}, \Delta {P_j}, \Delta {T_j} $$ (j=1,N)
Il bilancio tra numero di incognite e numero di equazioni mostra -
come dovevamo attenderci - che la soluzione richiede l'intervento
di quattro condizioni al contorno. Due di queste si ricavano
immediatamente osservando che al centro della struttura deve
risultare e rimanere $r = L$_r$ = 0$, e quindi
$\Delta {r_1} = 0, \Delta L_{r,1} = 0$
Restano dunque 4n-2 incognite. Le altre due condizioni risultano
dall'imporre che l'ultimo mesh (N) debba essere alla base dell'
atmosfera. Sappiamo infatti che le variabili fisiche alla base
dell'atmosfera sono note non appena sia assegnata una coppia di
valori L e Te. Per l'ultimo mesh devono valere dunque le
ulteriori condizioni
$$r_N = f_1(L,T_e)$$
$$L_{r,N} = f_2(L,T_e)$$
$$P_N = f_3(L,T_e)$$
$$T_N = f_4(L,T_e)$$
che aggiungono alle precedenti 4 nuove equazioni e due incognite
(L e Te). In totale abbiamo dunque un sistema di 4N equazioni
in 4N incognite, che viene in genere risolto per sostituzioni
successive ($\rightarrow$ A2.8), fornendo i valori delle
correzioni da apportare in ogni mesh alle funzioni di prova per
verificare le equazioni dell'equilibrio. Avendo nuovamente
linearizzato il problema, la soluzione sarà in genere raggiunta
tramite una serie di iterazioni, sempre che le funzioni di prova
siano assegnate all'interno di un'area di convergenza.
