A3.1 Eccitazione e ionizzazione: formule di Boltzmann e di Saha. Ionizzazione per pressione.
In accordo con i risultati della meccanica statistica all'equilibrio
termodinamico la popolazione
relativa di due stati separati da un'energia $\Delta E$
resta regolata dalla nota formula di Boltzmann
$$\frac {n_1}{n_0}= \frac {g_1}{g_0} e^{-\Delta E/kT}$$
dove $g_{0,1}$ rappresentano la degenerazione dei rispettivi stati,
cioè il numero di stati quantici sovrapposti nel medesimo
livello energetico. Nel caso di un generico atomo, r-volte
ionizzato, la formula di Boltzman regola la popolazione dei
diversi stati eccitati, ricordando che in assenza di campi
magnetici (trascurabilità dell'effetto Zeeman) ad ogni
stato con momento angolare $J_i$ corrisponde una degenerazione data
da $g_i= 2J_i+1$. Se quindi indichiamo con $E_i$ l'energia di
eccitazione del livello “i”, cioè l'energia che occorre fornire
per portarvi un elettrone dallo stato fondamentale, il popolamento
relativo di due qualunque stati eccitati $j$ e $k$ dello ione
sarà fornito dalla
$$\frac {n_j}{n_k}= \frac {g_j}{g_k} e^{-(E_j-E_k)/kT}$$
Sommando su tutti i possibili stati $j$ si ricava che la frazione
di ioni nello stato eccitato $k$ è data dalla relazione
$$ n_k = \frac {g_k e^{-E_k/kT}}{G}$$
dove
$$G = g_0 + g_1e^{-E_1/kT} + g_2e^{-E_2/kT}+ \ldots..$$
prende il nome di funzione di partizione dello ione.
Formule analoghe varranno per ogni specie atomica e per ogni
grado di ionizzazione.
Un qualunque ione isolato ha peraltro infiniti livelli eccitati, e la funzione di partizione diverge. Nel caso reale gli elettroni liberi si trovano nel campo di ioni ed elettroni. L'energia di elettrone libero nel plasma stellare diminuisce allora di un fattore $-e^2/R_D$ ove $R_D$ è il cosiddetto raggio di Debye e con esso diminuisce l'energia di ionizzazione. A causa di tale abbassamento del continuo il numero di livelli diventa finito e viene evitata la divergenza delle funzioni di partizione.
Analoghe considerazioni possono essere applicate ai processi
di ionizzazione. Dal bilancio energetico del prodesso di ionizzazione
di uno ione $A_r$ r volte ionizzato
$$A_r \rightarrow A_{r+1} + e$$
si può ricavare (equazione di Saha)
$$\frac {n_{r+1}n_e}{n_r}= \frac {G_{r+1}2}{G_r} (\frac {2
\pi m_e kT}{h^2})^{3/2} e^{-\chi_r/kT}$$
dove $\chi_r$ rappresenta l'energia necessaria per estrarre
un altro elettrone dall'atomo r-volte ionizzato.
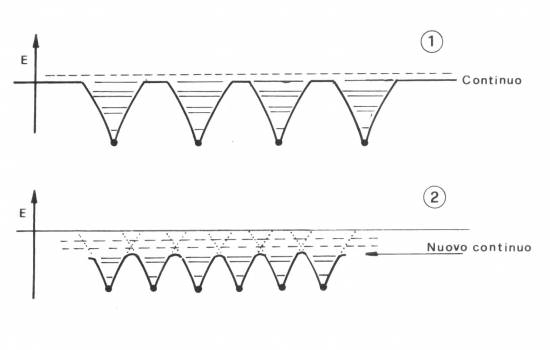
Figura 3.11 Schema del meccanismo di ionizzazione per
pressione. Atomi sufficientemente distanti si comportano come
buche di potenziale isolate (1) che ammettono tutta una serie di
livelli legati per gli elettroni. Avvicinandosi gli atomi (2) le
buche di potenziale tendono a fondersi, abbassando il livello del
continuo e distruggendo gli stati legati a energia superiore.
Al crescere della densità il raggio di Debye diminuisce e cresce
l'abbassamento del continuo. Calcoli dettagliati mostrano che a
densità dell'ordine di $10^3 gr/cm^3$ gli atomi di idrogeno
finiscono l'essere totalmente ionizzati: tale fenomeno prende il
nome di ionizzazione per pressione.
