I contributi alla pressione provengono dai tre componenti del plasma stellare: ioni, elettroni e radiazione elettromagnetica. La pressione totale sarà la somma dei contributi dovuti a tali componenti

$P=P_i+P_e+P_r$

con ovvio significato dei simboli. Si assume in ciò trascurabile il contributo di moti collettivi (convezione, turbolenza), la cui quantità di moto può peraltro giocare un ruolo non trascurabile nel caso delle atmosfere stellari.

3.2.1 Il gas perfetto

Per ciò che riguarda la componente particellare (ioni ed elettroni), in molti casi la materia stellare si comporta con buona od ottima approssimazione come un gas perfetto. Ricordiamo che per un gas perfetto di particelle libere e tra loro non interagenti, vale l'equazione di stato

$P=nkT$

ove $n$ è il numero di particelle per unità di volume e $k$ la costante di Boltzmann. Per la nostra miscela di ioni ed elettroni varrà quindi

$P=P_i+P_e= (n_i+n_e) kT$

Tale relazione può essere facilmente portata nelle due variabili $\rho,T$ (proprie delle equazioni di equilibrio), osservando che per un gas composto da particelle di massa “m” si ha

$n=\rho/m$

Poiché nel gas stellare la massa è essenzialmente quella degli ioni, potremo così porre

$P_i= \frac {k}{\mu_i H} \rho T$

dove $\mu_i$ è il peso molecolare degli ioni e H la massa dell'atomo di idrogeno. Il contributo degli elettroni viene introdotto attraverso l'artificio di definire un peso molecolare medio per elettrone $\mu_e= n_i/n_e$ ($=n_i/Z$ in caso di ionizzazione completa). Si ha così

$P_e=\frac {k}{\mu_e H} \rho T$

e, in totale

$P_{gas}= \frac {k}{\mu_i H} \rho T + \frac {k}{\mu_e H} \rho T = \frac {k}{\mu H} \rho T$

avendo posto $1/\mu = 1/\mu_i +1/\mu_e$.

Si noti come la valutazione della pressione degli elettroni richieda una valutazione dello stato di ionizzazione delle specie atomiche presenti ($\rightarrow A3.1$). Negli interni stellari è peraltro in generale lecito assumere la completa ionizzazione almeno delle due specie atomiche atomiche più abbondanti H e He. Troveremo infatti che stelle di sequenza principale hanno tipiche temperature centrali dell'ordine di $10-30 ~10^6$ K, cui corrisponde una radiazione largamente composta da fotoni di energia media $kT\sim 1 keV$ (raggi X duri). Poiché l'energia di ionizzazione dell'idrogeno è di soli 13.6 eV tale elemento sarà completamente ionizzato. Così è pure per l'He, i cui potenziali di prima e seconda ionizzazione risultano pari rispettivamente a 24.49 eV e 52.17 eV.

H e He saranno quindi completamente ionizzati nella maggior parte della materia stellare, eccettuate solo le parti più esterne ove la temperature scendono a valori di $10^3-10^4$ K. Ioni di atomi più pesanti sono invece in grado di conservare gli elettroni più interni anche a temperature elevate. L'energia di ionizzazione di un atomo idrogenoide (che ha cioè conservato un solo elettrone) risulta infatti pari a $W=Z^2m_e^4/2h^2$. Per il Ferro si ha così $W\sim 9 keV$, ed i nuclei di Fe saranno in grado di conservare in parte i loro elettroni più interni anche a temperature dell'ordine della decina di milioni di gradi.

Nel caso di ionizzazione completa è talora utile ricavare il numero di particelle per unità di volume dalle abbondanze in massa di idrogeno, elio ed elementi pesanti X, Y e Z. Per queste tre componenti il numero di nuclei ed il numero di elettroni si ottiene facilmente dalle relazioni

$n_H = X/H \rightarrow n_e = X/H$

$n_{He} = Y/4H \rightarrow n_e = Y/2H$

$n_{Zi} = X_i/A_i H \rightarrow n_e = X_iZ_i/A_iH$

dove con $X_i$ indichiamo l'abbondanza in massa dell' i-mo elemento pesante di numero atomico $A_i$ e carica $Z_i$. In totale si avrà dunque

$$n = (2X + \frac {3Y}{4} + \Sigma \frac {X_i}{A_i} + \Sigma \frac {X_i Z_i} {A_i })\frac {\rho}{H}$$

Trascurando $\Sigma X_i/A_i$ ($X_i<<1, A_i \geq 12$) ed osservando che $Z_i/A_i \sim 1/2$ (cioè esatto per C, N, O, Ne che sono tra i maggiori contributori a Z) si ottiene infine

$$n \simeq (2X + \frac {3Y}{4} +\frac {Z}{2})\frac {\rho}{H}$$

da cui per il peso molecolare medio ($\rho / \mu H = n$)

$$ \mu = \frac {1}{(2X + \frac {3Y}{4} + \frac {Z}{2}) }$$

Da queste relazioni si riconosce come, in prima approssimazione, il peso molecolare medio sia essenzialmente governato dalla ionizzazione di H e He, con un contributo solo marginale dei metalli (avendosi $Z\le 10^{-2}$).

3.2.2 Interazioni coulombiane e degenerazione elettronica

Per la componente particellare (ioni, elettroni) si può agevolemente verificare entro quali limiti l'energia cinetica predomina sulle interazioni coulombiane, condizione necessaria per poter assimilare il sistema ad un gas di particelle libere approssimanti un gas perfetto. Indicando con “d” la distanza media tra le particelle, per un gas di ioni con carica Ze la condizione si traduce ad esempio nella relazione

$kT $»$ Z^2e^2/d$ = E$_{Coul}$

Se $N_i$ è il numero di ioni per unità di volume, si ha anche

$N_i (=\rho/\mu H)\sim1/d^3$

dove $\mu$ è il peso molecolare degli ioni e H la massa dell'atomo di idrogeno. Se ne ricava

$d\sim 1/N^{1/3}\sim(\mu H/\rho)^{1/3}$

e la condizione si traduce nella relazione

$$T/\rho^{1/3}>> \frac {Z^2e^2}{k}\frac {1}{(\mu H)^{1/3}}$$

da cui

$\rho<<4 ~10^{-14}\mu T^3Z^6 gr/cm^3$

condizione in genere ben verificata nelle strutture stellari. Per temperature T$\sim10^7$ ∞K (combustione dell'idrogeno, Z=1) si ottiene $\rho<<4.10^7 gr/cm^3$, per T$\sim10^8$ (combustione dell'elio, Z=2) $\rho<<10^9 gr/cm^3$, cioè valori di densità che superano ampiamente quanto avremo occasione di verificare nella larga generalità delle strutture stellari. Le condizioni per un sensibile intervento di correzioni coulombiane (alte densità, basse temperature) appariranno solamente nel caso di stelle di piccola massa o di nane bianche, per le quali sarà necessario introdurre nell'equazione di stato opportuni termini di correzione coulombiana. Quando E$_{Coul} \sim$ kT il gas inizia a solidificare e per E$_{Coul} >$ kT gli ioni sono forzati in una struttura solida sino a cristallizzare (Fig.3.1).

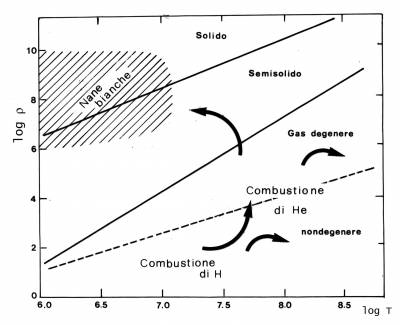
Figura 3.1 Mappatura schematica delle condizioni del plasma stellare al variare dei parametri temperatura-densità con schema delle traiettorie evolutive delle condizioni centrali di strutture stellari.

E' facile infine riconoscere che se sono trascurabili le interazioni ione-ione, lo sono anche quelle ione-elettrone ed elettrone-elettrone. Ciòè immediato per Z=1, mentre per Z maggiori la diminuzione del prodotto delle cariche interagenti prevale sulla contemporanea diminuzione delle mutue distanze.

Analoghe considerazioni consentono di investigare entro quali limiti il gas di particelle si può considerare libero da effetti quantistici, imponendo in questo caso che la distanza media tra le particelle risulti molto maggiore della lunghezza d'onda associata alle particelle medesime $\lambda = h/p$, dove p=mv rappresenta il momento delle singole particelle.

Per ioni ed elettroni, dall'equipartizione dell'energia si ha

$m_iv_i^2 = m_ev_e^2$

da cui si ricava immediatamente

$$\frac {m_iv_i}{m_ev_e} =\frac {v_e}{v_i}$$

che mostra come la quantità di moto degli ioni sia sempre molto maggiore di quella degli elettroni e, conseguentemente, che saranno in ogni caso gli elettroni ad entrare per primi in regime quantistico. Con considerazione del tutto analoghe a quelle già svolte per le interazioni coulombiane, dalla condizione

$\lambda = h /p << d$

osservando che $kT \sim m_ev_e^2$ e, quindi, $p^2 \sim m_ekT$, si ricava facilmente

$$\rho^{1/3}<< (\frac {\mu H}{Z})^{1/3} \frac{(m_ekT)^{1/2}}{h}$$

$\rho<< 10^{-10}T^{1/2} gr/cm^3$

Ove ciò non si verifichi, si manifestano effetti quantistici ed il gas di elettroni viene definito quantisticamente degenere. E' immediato riconoscere come queste condizioni sulla densità siano più stringenti di quelle per le interazioni coulombiane. In effetti la degenerazione elettronica giocherà un ruolo determinante in molte strutture stellari.

3.2.3 Equazione di stato del plasma stellare

Se alla pressione del gas aggiungiamo il contributo portato dalla radiazione, ove non intervengano fenomeni di degenerazione elettronica e risultino trascurabili le interazioni coulombiane, otteniamo l'equazione di stato per il plasma stellare

$$P = \frac {k}{H} \rho T (\frac {1}{\mu_i} + \frac {1}{\mu_e}) + \frac {a}{3} T^4 $$

Gli effetti della degenerazione elettronica sono di rendere il gas di elettroni più incomprimibile di un gas perfetto. Gli elettroni sono infatti fermioni (cioè particelle a spin semintero) per i quali vale il principio di esclusione di Pauli per il quale non più di due elettroni possono occupare un identico stato energetico. Ne segue, ad esempio, che nel limite $T \rightarrow 0$ un gas di elettroni possiede energia e quantità di moto, quest'ultima implicando una pressione non prevista dalla trattazione classica.

Si può porre

$$P_e = P_e + P_{e,d}$$

ove con $P_e$ e $P_{e,d}$ si indicano rispettivamente la pressione di un gas perfetto di elettroni e il contributo della digenerazione. $P_{e,d}$ può essere calcolato sulla base del comportamento quantistico di un gas di Fermi (<tex>$\rightarrow A3.2$</tex>). La Figura 3.2 mostra l'intervento della degenerazione nel piano $\rho$, T, riportando in particolare la linea di transizione lungo la quale $P_{e,d}=P_e$, come definita dalla relazione

$$ \rho/\mu_e = n_e = 2.4 10^{-8}T^{3/2} cm^{-3}$$

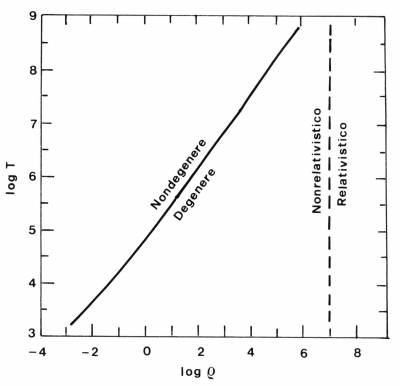
Figura 3.2 La linea del piano $log T$, $log \rho$ lungo la quale la pressione di degenerazione eguaglia quella degli elettroni liberi. La linea a tratti segnala l'instaurarsi di degenerazione relativistica.

In caso di completa degenerazione ($P_{e,d}>> P_e$) la pressione del gas è data dai soli elettroni degeneri ($P_e > P_i$), dipendendo in tal caso solo dalla densità secondo la relazione (c.g.s.)

$$P_g = P_e = 10.00~ 10^{12}(\rho/\mu_e)^{/3} $$

Per altissime densità ($\rho \ge 10^7$) la degenerazione spinge gli elettroni in livelli energetici così alti che l'energia non è più trascurabile rispetto all'energia della massa a riposo ($m_ec^2$) rendendo necessaria una trattazione relativistica. In tal caso per la quantità di moto si avrà

$p_e = m_ev/(1-v^2/c^2)^{1/2}$ ($\sim m_e v$ se $v«c$)

e per la pressione si ha

$$P_g = P_e = 6.58 * 10^14 (\rho/\mu_e)^{4/3}$$