Indice
3.4 Generazione di energia
Nelle equazioni dell'equilibrio la condizione di conservazione
dell'energia interviene attraverso il coefficiente $\varepsilon$,
inteso come bilancio energetico per grammo di materia e per
secondo. I meccanismi che possono contribuire a tale bilancio sono
tre, cuiè d'uso far corrispondere i tre distinti coefficienti:
$\rightarrow \varepsilon_g:$
Trasformazioni termodinamiche della
materia,
$\rightarrow \varepsilon_N:$ Produzione di energia per reazioni di
fusione nucleare,
$\rightarrow \varepsilon_\nu:$ Perdita di energia per produzione
di neutrini.
Il coefficiente di produzione di energia risulta ovviamente
definito come somma dei relativi contributi:
$$\varepsilon = \varepsilon_g + \varepsilon_N -\varepsilon_{\nu}$$.
3.4.1 Il bilancio termico della materia
Al primo meccanismo corrisponde il calore assorbito o prodotto a
causa delle trasformazioni termodinamiche subite dalla materia
stellare. Di norma indicato, ma impropriamente, come produzione
di energia gravitazionale, in esso deve essere compreso non solo
il lavoro delle forze di pressione ma anche le variazioni di
energia interna del plasma stellare. Il bilancio termico per
grammo di materia è immediatamente fornito dal primo principio
della termodinamica che con formulazione intensiva può essere
scritto
$$dQ = dU +p d(1/\rho)$$
dove U rappresenta l'energia interna per grammo di materia e
1/$\rho$ è il volume corrispondente. Introducendo l'entropia per
grammo di materia S si ricava
$$ \varepsilon_g = -\frac {dQ}{dt} =
-T \frac {dS}{dt}=- T [(\frac {dS}{dP})_T \frac {dP}{dt}+ (\frac
{dS}{dT})_P \frac {dT}{dt}] = E_P \dot P - C_P \dot T$$
I coefficienti $E_P$ e $C_P$ delle derivate temporali sono
facilmente ricavabili nel caso di una miscela di gas perfetto e
radiazione ($\rightarrow A2.4$). Nel caso generale essi vengono
calcolati assieme all'equazione di stato e forniti anch'essi sotto
forma tabulare. Si noti come la presenza delle derivate temporali
implichi che laddove $\varepsilon_g$ non sia nullo l'integrazione
di una struttura stellare richiede precise informazioni sulla
passata storia temporale di P e T lungo tutta la struttura della
stella.
3.4.2 Energia Nucleare
Ad alte temperature due o più nuclei leggeri possono arrivare in
contatto, fondendosi per formare un nucleo più massiccio con un
rilascio di energia ($"Q"$ della reazione) dato dalla differenza
tra le masse iniziali e quelle dei prodotti di reazione secondo la
nota relazione $E=mc^2$. E' subito da notare al proposito che in
natura la massa media per nucleone decresce al crescere del numero atomico
A dall'idrogeno sino al nucleo del Ferro (Fe), per risalire
progressivamente per A ancora maggiori. Se ne ricava che per il Fe
è massima l'energia di legame per nucleone (Fig. 3.7) cioè
l'energia che occorre fornire ai
nucleoni per portarli allo stato libero e, quindi, alle masse
caratteristiche dei nucleoni liberi. Ne segue anche che reazioni
di fusione nucleare sono esoenergetiche sino alla formazione di
Fe. La fusione di due nuclei di Fe, ad es., richiederebbe invece
l'assorbimento dell'energia necessaria per portare i nucleoni alla
maggiore massa. Si comprende così come per elementi pesanti,
quale l'Uranio, risultino esoenergetiche non le reazioni di
fusione
ma quelle di fissione, cioè di rottura del nucleo
in due o più frammenti.
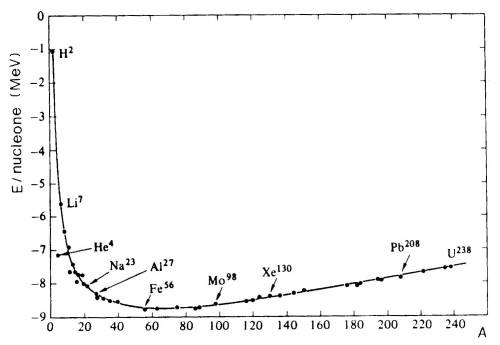
Figura 3.7 L'energia di massa per nucleone al variare
del numero di nucleoni (numero atomico) in nuclidi stabili.
L'energia ceduta da una reazione si presenta sotto forma di
energia dei prodotti di reazione. Se osserviamo una tipica
reazione di fusione di interesse stellare (fusione di due protoni
(p) in un nucleo di deuterio (D))
$$p + p \rightarrow D + e^+ + \nu_e$$
troviamo l'energia rilasciata sotto forma di energia cinetica dei
prodotti di reazione e nella produzione dell'elettrone positivo.
Quest'ultima particella è destinata ad annichilarsi con un
elettrone negativo
$$e^+ +e^- \rightarrow 2\gamma$$
così che la produzione del positrone corrisponde, come bilancio
netto energetico, alla produzione di due $\gamma$ di energia
complessiva pari all'energia delle masse a riposo degli elettroni
annichilati ($2m_ec^2$) più l'energia cinetica delle due
particelle.
Il $\gamma$ ed il deutone D vengono rapidamente termalizzati,
cedendo così la loro energia alla struttura. Questo non
avviene per il neutrino elettronico $\nu_e$, particella debole il
cui cammino libero medio è ben superiore alle dimensioni
stellari. L'energia $Q^*$ acquisita dalla struttura è quindi
fornita dal $Q$ della reazione meno l'energia (media) portata dal
neutrino. Ove sia noto il numero N di reazioni nucleari che
avvengono per unità di tempo e di volume, il coefficiente di
energia nucleare sarà fornito, per ogni prefissata reazione,
dalla relazione
$$\varepsilon_N = \frac {N}{\rho}Q^* \ erg \ gr^{-1} \ sec^{-1}$$
3.4.3 Termoneutrini
Ad alte temperature e densità, a fianco della produzione di
neutrini nelle reazioni nucleari divengono efficienti meccanismi
di produzione di neutrini direttamente a spese del contenuto
termico del plasma stellare, cui nel seguito daremo il nome di
termoneutrini. La teoria delle interazioni deboli fornisce
il quadro di tali interazioni quali provengono anche dalla provata
esistenza di correnti neutre :
$$e^-+(Z,A) \rightarrow e^-+(Z,A)+\nu_e+\overline \nu_e \ (br\ddot{a}mstrahlung)$$
$$\gamma+e^- \rightarrow e^-+\nu_e+\overline \nu_e \ (fotoproduzione)$$
$$\gamma \rightarrow e^++e^- \rightarrow \nu_e+ \overline
\nu_e \ (da \ coppie)$$
dove tra i processi di Bremsstrahlung è da
comprendere anche l'interazione elettrone-elettrone.
E' facile riconoscere come tali processi rappresentino l'analogo
di noti processi che coinvolgono elettroni e fotoni, ove si
ammetta in uscita una coppia neutrino-antineutrino al posto di
fotoni.
$$e^-+(Z,A) \rightarrow e^-+(Z,A)+\gamma \ (br\ddot{a}mstrahlung)$$
$$\gamma+e^- \rightarrow e^-+\gamma \ (scattering)$$
$$\gamma \rightarrow e^++e^- \rightarrow \gamma+\gamma \ (creazione \ e \ annichilazione \ di \ coppie)$$
A densità elevate diviene inoltre efficiente un altro e più
complesso canale di produzione di termoneutrini: i neutrini
da oscillazione di plasma. Per delinearne il meccanismo,
ricordiamo come un fotone non possa decadere direttamente in una
coppia di neutrini non potendosi conservare energia e quantità
di moto. Da qui l'intervento nei processi di braemstrahlung e di
fotoproduzione di un ulteriore particella. Fotoni in un gas
ionizzato, quale è l'interno stellare, possono interagire anche
con i modi di oscillazione del plasma (la cui quantizzazione
conduce al concetto di plasmone) scambiando quantità di
moto e divenendo in grado di produrre coppie di neutrini.
La teoria delle interazioni deboli consente di valutare l'efficienza dei vari processi, giungendo così a valutare l'energia depositata in questi neutrini. Si noti come in questi fenomeni, che definiremo di termoproduzione, i neutrini giocano un ruolo differente da quanto già esaminato nel caso dei neutrini da reazioni di fusione nucleari. Nella fusione infatti i neutrini semplicemente “taglieggiano” l'energia prodotta nella fusione, diminuendone l'efficienza che resta peraltro positiva. Nella termoproduzione il neutrino sottrae invece energia direttamente dalla struttura stellare, realizzando un meccanismo di raffredamento che ha fondamentali ripercussioni nella storia evolutiva di molte strutture stellari.
La figura 3.8 riporta una mappatura nel piano
$\rho,T$ dell'efficienza relativa dei vari processi di produzione.
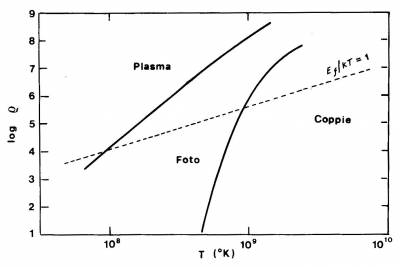
Figura 3.8 Regioni del piano($\rho$, T) di predominio
dei diversi processi di produzione di termoneutrini. E' mostrata,
a tratti, la linea lungo la quale l'Energia di Fermi (E$_f$)
eguaglia l'energia termica, che delimita la regione di
degenerazione elettronica.
