4.4 Elementi primari ed elementi secondari
Chi avesse dimestichezza con le famiglie di elementi radioattivi naturali riconoscerebbe nella catena pp tutta una serie di elementi “secondari”, i cui nuclei sono contemporaneamente prodotti e distrutti nella sequenza di reazioni. In tale condizione le abbondanze di questi elementi tendono verso condizioni di equilibrio, ed i nuclei non intervengono più nel determinare la velocità delle reazioni se non in maniera indiretta. Illustreremo tale caratteristica nel caso del deuterio.
Per il deuterio si ha infatti una reazione di produzione
$(p+p\rightarrow)$ ed una di distruzione $(D+p\rightarrow)$.
Poichè per ogni reazione viene creato o distrutto un nucleo di
deuterio, il numero di nuclei creati o distrutti nell'unità di
volume e nell'unità di tempo sarà dato dalle relazioni
$$ Processi \ di \ creazione \rightarrow
\frac{dN_2}{dt}=n_{1,2}=\frac{N_1^2}{2}<\sigma_{11}v>$$
$$ Processi \ di \ distruzione \rightarrow \frac{dN_2}{dt}= -n_{12}=
-N_1N_2<\sigma_{12}v>$$
dove 1 e 2 fanno riferimento rispettivamente a protoni e deutoni.
Ne segue che che il numero di deutoni nell'unità di volume
varia col tempo secondo la relazione
$$\frac{dN_2}{dt}=n_{11}-n_{12}$$
Qualunque sia l'abbondanza iniziale del deuterio (ma in
realtà ce ne attendiamo molto poco) si ricava che l'abbondanza
di tale elemento deve evolvere verso la condizione di equilibrio
$$n_{11}=n_{12}$$
da cui si trae per le abbondanze di equilibrio
$$(\frac{N_2}{N_1})_{eq}=\frac{1}{2} \frac{<\sigma_{11}v>}{<\sigma_{12}v>}$$
E' subito visto infatti che se $N_2>N_1$ allora
$\sigma_{12}>\sigma_{11}$, e viceversa, così che le
abbondanze evolvono necessariamente verso l'equilibrio. Ricordando
che le abbondanze in numero sono legate a quelle in massa dalla
relazione $X_i=N_iA_iH/\rho$ per le abbondanze in massa di
equilibrio potremo scrivere
$(X_2/X_1)_{eq}=<\sigma_{11}v>/<\sigma_{12}v>$
Si può ottenere una scala dei tempi per il raggiungimento
dell'equilibrio osservando che, per esempio, se $N_2\gg
(N_2)_{eq}$ prevale la reazione di distruzione, per la quale
$$\frac{1}{N_2}\frac{dN_2}{dt}=\frac{d}{dt}lnN_2=-N_1<\sigma_{12}v>$$
da cui $N_2=N_2^0 e^{-t/\tau}$ con $\tau=1/(N_1<\sigma_{11}v>)$.
Per una miscela ricca di idrogeno e per temperature in cui la
fusione pp è efficiente si trova così $(X_2)_{eq}\le
10^{-18}, \tau \le 1$ secondo. Le condizioni di equilibrio sono
cioè raggiunte in tempi rapidissimi e senza una apprezzabile
variazione della composizione chimica della materia (Figura 4.3).
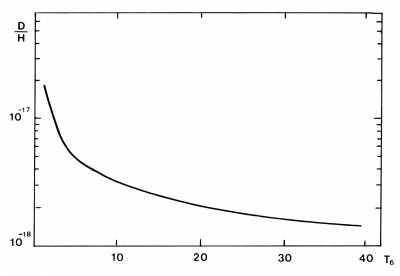
Fig. 4.3 Il rapporto di equilibrio D/H al variare
della temperatura T in milioni di gradi.
All'equilibrio ogni reazione p+p è necessariamente seguita da
una reazione D+p, talchè si può direttamente assumere che
ogni reazione p+p abbia per risultato la scomparsa di tre protoni
e la sintesi di un nucleo di $^3He$, la velocità di produzione
restando regolata solo dal valore di $n_{11}$. In questo senso il
deuterio è elemento secondario, come lo sono anche $^7Be$,
$^7Li$, $^8Be$, $^8B$ la cui dettagliata valutazione risulta
inessenziale sia ai fini della evoluzione chimica che a quelli
della produzione di energia della catena pp, fermo restando che
alle restanti reazioni primarie occorrerà associare i
prodotti in particelle ed i contributi energetici provenienti
dalle reazioni secondarie che le seguono.
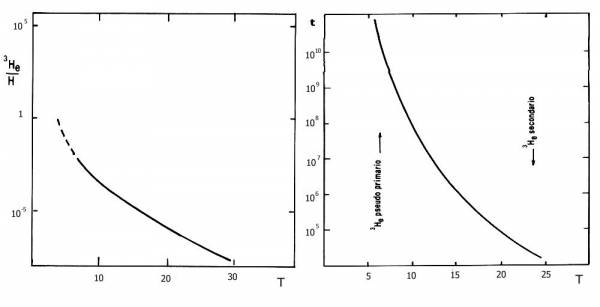
Fig. 4.4 La concentrazione all'equilibrio di <tex>$^3$He</tex>
(a sinistra) e il tempo (in anni) per raggiungere l'equilibrio
stesso (a destra) in funzione della temperatura in milioni di
gradi.
Così gli effetti delle due prime reazioni della catena
$p+p\rightarrow D+e^++\nu \ (+Q_{11})$
$D+p\rightarrow ^3He+\gamma \ (+Q_{12})$
ove con $Q_{ii}$ indichiamo l'energia rilasciata nella
singola reazione eventualmente decurtata della enrgia sotto forma
di neutrini,restano compiutamente descritti dalle relazioni
$$\frac{dN_1}{dt}=-3 n_{11} \ \frac{dN_3}{dt}= n_{11}$$
$$\frac{dQ}{dt}= n_{11}(Q_{11}+Q_{12})$$
ove le prime due regolano, con ovvio significato dei simboli, la
variazione col tempo del numero di particelle per unità di
volume e la terza fornisce l'energia prodotta per unità di
tempo sempre nell'unità di volume. Da quest'ultima si ricava
immediatamente la produzione di energia per grammo e per secondo
della ppI:
$$\varepsilon =\frac{1}{\rho}\frac{dQ}{dt}$$
Resta da notare che alcuni elementi, come nel nostro
caso l'$^3He$, possono comportarsi da primari o secondari a
seconda della temperatura che regola il valore della sezione
d'urto di distruzione. A basse temperature la sezione d'urto
$^3He+^3He$ è molto piccola e la composizione d'equilibrio
-sempre esistente- è corrispondentemente non solo molto alta
ma anche raggiunta in tempi lunghi. L'evoluzione dell'abbondanza
di $^3He$ deve quindi essere seguita in dettaglio e l'$^3He$ si
comporta come elemento pseudoprimario. Al crescere della
temperatura aumenta la sezione d'urto di distruzione e l'$^3He$
diviene a tutto rigore un secondario (Fig. 4.4).
