A4.1 La formazione stellare. Funzione iniziale di massa (IMF)
La formazione stellare origina dal prevalere della gravità sulla agitazione termica del gas interstellare. La dinamica dei processi di formazione è peraltro ancora aperta a indagini ed ipotesi. Per quel che riguarda l'identificazione del meccanismo che conduce nubi interstellari a superare la massa critica, iniziando la contrazione, sono possibili due scenari:
- La massa critica viene superata per fluttuazioni spontanee nella densità e/o per raffreddamento del gas,
- La massa critica viene superata a causa della compressione prodotta dalla propagazione nel mezzo di onde d'urto prodotte da una vicina supernova.
Tali due meccanismi, anzichè essere alternativi, possono rappresentare due meccanismi concorrenziali che, con efficienza da determinare, hanno contribuito alla formazione stellare lungo l'arco della storia della nostra Galassia. In tale contesto, le più volte citate differenze tra ammassi stellari di disco e di alone (numero di stelle e stato dinamico) sono indice di una sostanziale differenza nello stato fisico del gas nel quale si formarono i protoammassi e/o nei meccanismi di formazione.
Nel primo caso (fluttuazioni spontanee) la produzione di stelle resta indipendente dalla presenza in loco di altre stelle,o tutt'al più inibita da tali stelle se esse, riscaldando il gas, elevano il valore della massa di Jeans. In tal caso ci si attendono processi di formazione stellari più o meno casualmente scaglionati nel tempo. La formazione di stelle indotta da eventi di Supernova suggerisce al contrario che la nascita di sistemi stellari sia un evento autopropagantesi: la formazione di un sistema stellare implica la presenza di stelle massicce che, esplodendo come Supernove, inducono in sequenza la formazione di ulteriori sistemi stellari nelle regioni circostanti, e così di seguito. Un processo iterativo di cui si trova forse evidenza osservativa nella sequenza temporale di alcuni gruppi di ammassi aperti della Galassia.
La distribuzione di masse stellari risultante al termine della
gerarchia di frammentazioni di un protoammasso è un problema
fondamentale tuttora aperto. Dall'osservazione delle stelle
attorno al Sole è stata a suo tempo (1955) ricavata per tale
distribuzione una legge di potenza, nota come IMF
(Initial Mass Function) di
Salpeter, fornita in letteratura nelle due forme
alternative:
$$ \frac {dN}{dlnM}= M \frac {dN}{dM}= M^{-\alpha}= M^{-1.35}$$
$$ \frac {dN}{dM}= M^{-(\alpha+1)}= M^{-2.35}$$
E' subito visto come tale distribuzione diverga per
M → 0: essa era infatti intesa a descrivere la
distribuzione della IMF per masse superiori o dell'ordine di 1
M$_{\odot}$. Le più recenti evidenze osservative mostrano che
la distribuzione di Salpeter può al più essere mantenuta sino
a masse dell'ordine di 0.6 M$_{\odot}$; per masse minori sono
state proposte varie alternative, tutte in accordo nell'abbassare
drasticamente il numero di stelle previsto in tale intervallo di
masse. Miller e Scalo (1979) hanno ad esempio proposto di interpretare i
dati osservativi in termini di una distribuzione log-normale, del
tipo
$$\frac {dN}{dlnM} \propto exp[-C_1(logM-C_2)^2] $$
con cui coprire l'intero intervallo di masse. Non
è peraltro ancora chiaro il ruolo dei fenomeni fisici alla base
di una tale distribuzione, nè - in particolare - quanto tale
legge sia di validità generale o rappresenti - al contrario -
una distribuzione caratteristica delle sole stelle di Popolazione
I. L'ipotesi che la IMF dipenda anche sensibilmente dal contenuto
di metalli è stata infatti avanzata più volte, sulla base
dell'osservazione che il contenuto di metalli condiziona
l'opacità della materia ed i meccanismi di raffreddamento della
medesima, processi che dovrebbero giuocare un ruolo non
trascurabile nella dinamica della contrazione e della
frammentazione.
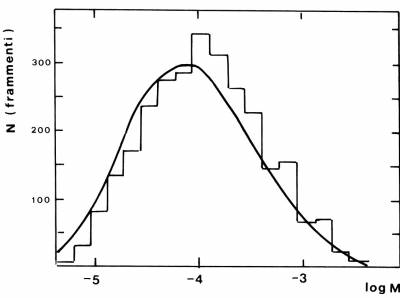
Fig. 4.13 Istogramma della distribuzione in massa dei
frammenti risultanti da un processo probabilistico confrontato con
una distribuzione log-normale. Le masse sono in frazioni della
massa della nube iniziale.
E' interessante peraltro notare come sia stato mostrato che una
distribuzione log-normale sia spontaneamente raggiunta quando si
supponga che il processo di successive frammentazioni sia retto
da leggi probabilistiche per quel che riguarda il numero di
frammenti per evento, le masse di tali frammenti e il numero di
frammentazioni (Fig. 4.13)
