5.5. La Sequenza Principale di Età Zero (ZAMS)
In base alle considerazioni evolutive sin qui svolte è possibile
produrre valutazioni teoriche sulle strutture di Sequenza
Principale per ogni assunta composizione chimica iniziale. La Fig. 5.8
riporta, nel riquadro a sinistra, l'andamento nel
diagramma HR di tali sequenze per tre scelte di composizione
chimica che coprono le composizioni delle strutture galattiche. Il
riquadro a destra nella stessa figura riporta l'andamento delle
temperature centrali per gli stessi modelli.
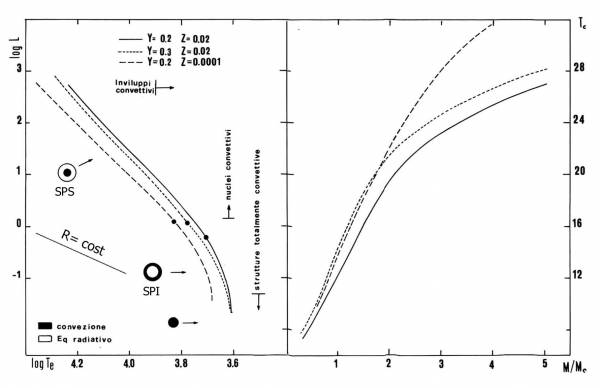
Fig. 5.8 A sinistra: distribuzione nel diagramma HR
di strutture di sequenza principale per le indicate composizioni
chimiche. Il punto lungo le sequenze segnala la collocazione dei
modelli di 1 M$_{\odot}$. E' indicata una retta R= cost (logL
$\propto$ 4logT$_e$). A destra: andamento delle temperature
centrali (in milioni di gradi) al variare della massa negli stessi
modelli.
Luminosità e temperatura centrale crescono in ogni caso al
crescere della massa, come richiesto dal crescente contenuto
energetico e conseguente fabbisogno delle strutture di equilibrio.
Al crecere della massa stellare segue l'inevitabile passaggio
delle combustioni nucleari sotto il controllo del ciclo CNO. La
transizione tra catena pp e ciclo CNO avviene attorno alle 1-2
M$_{\odot}$, in dipendenza anche dalla composizione chimica. Tale
transizione è segnalata dalla diversa pendenza della relazione
massa - temperatura centrale: per sostenere l'aumento di
luminosità con la crescita della massa, stelle sorrette dalla
catena pp ($ \propto T^4$) devono aumentare la temperatura
centrale molto più rapidamente di quanto richiesto dalle stelle
sorrette dal ciclo CNO, a motivo della molto maggiore dipendenza dalla
temperatura di queste ultime ($ \propto T^{14}$).
Le masse minori, sorrette dalla catena pp, come conseguenza della bassa dipendenza di tale catena dalla temperatura hanno nuclei in equilibrio radiativo, con l'occasionale e transitoria presenza di una limitata convezione da $^3$He ($\rightarrow A5.3$). La alta dipendenza dalla temperatura del ciclo CNO genera invece nuclei convettivi che aumentano all'aumentare della massa e, quindi, della temperatura centrale. Contemporaneamente, stelle a massa minore si collocano a temperature effettive corrispondentemente minori, ove abbiamo visto debbano svilupparsi inviluppi convettivi che devono scomparire alle alte temperature efficaci. Ne segue che -come indicato in figura- stelle della Sequenza Principale “Inferiore” (SPI) o “Superiore” (SPS) hanno strutture caratteristicamente speculari: nuclei radiativi ed inviluppi convettivi le prime, nuclei convettivi e inviluppi radiativi le seconde. Differenze che si rifletteranno nelle successive fasi evolutive. La convezione superficiale, presente a partire da logT$_e \sim$ 4.0, a logT$_e \sim$ 3.8 comincia ad interessare consistenti frazioni di massa stellare, affondando sempre di più al diminuire della massa (e della temperatura efficace) sino a produrre per masse M$\le$ 0.3 M$_{\odot}$ strutture totalmente convettive.
La Tabella 1 riporta alcune grandezze caratterizzanti strutture di sequenza principale con composizione originale solare, Z=0.02, Y=0.27. Si nota come, in generale, al crescere della massa decresca sensibilmente la densità centrale. Si può comprendere il significato di tale comportamento ricorrendo alla condizione di equilibrio imposta dal viriale. Supponiamo infatti di avere una fissata struttura stellare e di aumentarne (con un gedanken experiment) la massa. La struttura ha due vie per ritrovare l'equilibrio: aumentare l'energia cinetica totale (aumentare la temperatura) o diminuire l'energia gravitazionale (espandere e diminuire la densità). I dati in tabella mostrano che le strutture stellari sfruttano contemporaneamente ambedue i canali. La leggera deviazione da tale comportamento generale attorno 1 M$_{\odot}$ è, forse, da porsi in connessione con la transizione tra i due tipi di combustione e la nascita dei nuclei convettivi. Se, aumentando la massa, aumenta la temperatura e diminuisce la densità dobbiamo infine concluderne che all'aumentare della massa le strutture si allontanano sempre più dal rischio di degenerazione elettronica, accadimento che è la chiave di volta dalla quale dipenderanno le caratteristiche dell'evoluzione delle strutture nelle fasi successive alla Sequenza Principale.
| M | logL | logTe | R | Tc | $\rho_c$ | Mcc | Mce | Lpp | LCNO | tH |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | -3.06 | 3.450 | 0.12 | 4.69 | 402.5 | compl. | conv. | 1.000 | 0.000 | $\sim$1000 10$^9$ |
| 0.3 | -1.98 | 3.534 | 0.29 | 7.69 | 100.7 | compl. | conv. | 1.000 | 0.000 | $\sim$500 10$^9$ |
| 0.6 | -1.09 | 3.620 | 9.55 | 10.0 | 84.7 | 0.04 | 0.510 | 0.996 | 0.004 | 73 109 |
| 0.8 | -0.59 | 3.694 | 0.70 | 11.7 | 79.2 | 0.06 | 0.741 | 0.980 | 0.020 | 23 109 |
| 1.0 | -0.17 | 3.751 | 0.87 | 13.7 | 77.4 | 0.07 | 0.969 | 0.898 | 0.136 | 10 109 |
| 1.5 | 0.69 | 3.849 | 1.49 | 18.1 | 79.4 | 0.07 | 0.981 | 0.803 | 0.168 | 2.2 109 |
| 2.5 | 1.59 | 4.028 | 1.84 | 22.7 | 48.9 | 0.44 | – | 0.277 | 0.724 | 497 106 |
| 5.0 | 2.74 | 4.230 | 2.73 | 26.9 | 20.3 | 0.94 | – | 0.033 | 0.967 | 83 106 |
| 7.0 | 3.25 | 4.318 | 3.27 | 29.1 | 13.5 | 1.60 | – | 0.013 | 0.987 | 38 106 |
Tabella 1 Grandezze caratteristiche di alcune strutture di ZAMS per
composizione chimica solare. Vengono riportati nell'ordine: la
massa M in masse solari, luminosità e temperatura effettiva,
raggio in raggi solari, temperatura Tc e densità centrale
$\rho_c$, la massa del nucleo convettivo Mcc in masse solari,
la frazione di massa del bordo inferiore della convezione esterna
Mce e la frazione di energia prodotta tramite la catena pp o
il ciclo CNO. L'ultima colonna riporta infine il tempo, in anni,
che le strutture trascorreranno nella fase di combustione centrale
di H.
Per quel che riguarda le strutture di MS, la degenerazione
elettronica comincia ad influire solo nelle stelle al di sotto di
1 M$_{\odot}$, crescendo al diminuire della massa, sinché
attorno a 0.1 M$_{\odot}$ giunge a bloccare la contrazione di
presequenza e ad impedire così l'innesco della combustione
dell'idrogeno. Strutture al di sotto di tale limite continueranno
a raffreddare sotto forma di oggetti compatti sorretti dalla
pressione di degenerazione, dissipando il calore prodotto nella
fase gravitativa. Se non troppo al di sotto della massa limite, a
queste “stelle mancate” si dà il nome di Nane Brune (Brown
Dwarfs) ad indicare l'esistenza di sia pur limitate capacità
radiative. Con masse ancora minori si entra nel campo dei pianeti
gassosi, con analoga storia evolutiva. In tale contesto è da
notare come nel nostro sistema planetario Giove, M$_J \sim$
10$^{-3}$ M$_{\odot}$, emetta una quantità di energia maggiore
di quella ricevuta dal Sole, una evidenza da porsi forse in
relazione con una residua lenta contrazione.
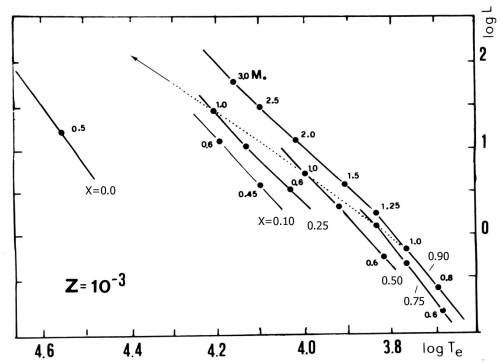
Fig. 5.9 La collocazione nel diagramma HR di
Sequenze Principali con Z=0.001 e varie assunzioni sull'abbondanza
di idrogeno X. La linea a punti mostra il luogo di modelli di
1M$_{\odot}$ al variare di X.
La Fig. 5.8 mostra come al diminuire del contenuto di
metalli e/o all'aumentare del contenuto di elio le sequenze
principali si spostino verso maggiori temperature effettive,
mentre a parità di massa le strutture risultano più luminose.
Questa ultima evidenza indica senza ambiguità un aumento delle
temperature centrali, come peraltro verificabile nel riquadro
destro della stessa figura. Notiamo subito che la dipendenza della
collocazione nel diagramma HR dal contenuto di elementi pesanti
rende ragione della collocazione in tale diagramma delle subnane
di campo, le stelle povere di metalli che transitano nelle
vicinanza del Sole ($\rightarrow$ Cap.1). L'aumento della
luminosità lascia anche prevedere che al diminuire del contenuto
di metalli diminuisca anche la durata, a parità di massa, della
fase di combustione di idrogeno.
La risposta delle strutture alle variazioni di elio può essere compresa osservando che, a parità di densità, l'incremento della percentuale di elio diminuisce il numero di particelle: la struttura deve contrarre e aumentare la sua temperatura per contrastare l'aumentata gravitazione. Ogni volta che si aumenta il peso molecolare, troveremo strutture più calde e più luminose. La Fig. 5.9 riporta una estesa analisi della collocazione delle Sequenze Principali al variare del contenuto di elio. Spingendosi verso il limite X (abbondanza di idrogeno)$\rightarrow$0 le sequenze coprono una vasta ma limitata fascia del diagramma H R, per balzare a temperature efficaci notevolmente più alte per X=0. Tale balzo è collegato alla variazione nel meccanismo di combustione che, all'esaurimento dell'idrogeno, deve passare dalla combustione di tale elemento alla combustione 3$\alpha$, che richiede temperature centrali molto maggiori.
Si noti che se le stelle fossero oggetto di efficienti rimescolamenti interni evolverebbero mantenendosi omogenee, accrescendo col tempo il loro contenuto di elio. La loro traccia evolutiva dovrebbe dunque seguire le linee a massa costante in Fig. 5.9, spostandosi sulla sinistra della Sequenza Principale. Tale approccio topologico fornisce una semplice risposta ad un delicato problema: l'evidenza di rotazione delle strutture stellari può lasciar sospettare che fenomeni di circolazione meridiana rimescolino la struttura, mantenendola omogene. La valutazione teorica dell'efficienza di tali rimescolamenti è collegata a non semplici valutazioni sulla viscosità del gas stellare, e potrebbe apparire dubbia. La riposta osservativa è esplicitamente e inconfutabilmente negativa, mostrando che l'evoluzione sposta le strutture non sulla sinistra ma sulla destra della Sequenza Principale. Sarà dunque l'evoluzione disomogenea a dover rendere conto degli osservabili, cosa che farà con buon successo. Conviene peraltro ancora una volta ricordare come l'incertezza sulla lunghezza di rimescolamento si traduca in una indeterminazione sul valore della temperatura efficace in stelle con inviluppi convettivi i cui effetti dovrano essere opportunamente valutati.
La Fig. 5.10 riporta l'andamento delle variabili
fisiche e di composizione in un modello di MS di 1.25 M$_{\odot}$.
Si noti in particolare l'evidente presenza di un piccolo nucleo
convettivo e l'evoluzione dei diversi elementi chimici che
intervengono nelle due combustioni pp e CNO. La caratteristica
distribuzione dell'$^3$He corrisponde al fatto che nelle zone
più interne questo elemento ha ormai raggiunto la sua abbondanza
di equilibrio (che cresce al diminuire della temperatura) mente
nelle zone più esterne non è stato ancora formato.
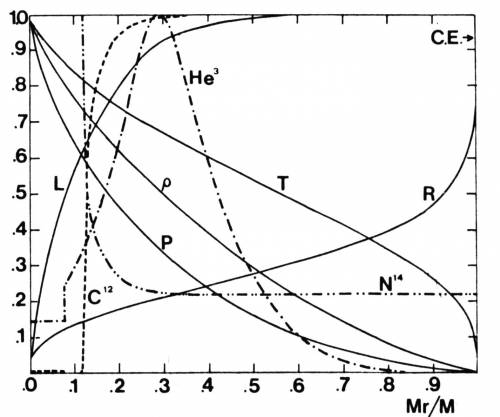
Fig. 5.10. Andamento con la frazione di massa delle
variabili fisiche e chimiche in un modello di MS di 1.25
M$_{\odot}$, Z=0.001, Y=0.1. Le variabili sono normalizzate ai
valori L=7.16 1033 erg/sec, P=2.05 1018 dyn/cm2,
$\rho$=87.81, T=14.88 106 K, R=6.84 1011 cm, X3=6.37
10-4, X12=1.41 10-4, X14=2.41 10-4.
Qui come sempre nel seguito, occorre ricordare come la
indeterminazione sulla lunghezza di rimescolamento si traduca in
una indeterminazione sui valori assoluti delle temperature con
inviluppi convettivi ($\rightarrow$ A6.1), indeterminazione che
è necessario tenere in considerazione ogniqualvolta si proceda
all'interpretazione di dati osservativi.
