La collocazione nel diagramma HR delle stelle di un ammasso stellare deve essere considerata come il luogo, ad un prefissato tempo t₀ (isocrona), dei punti rappresentativi di stelle in moto lungo traiettorie prefissate (le tracce evolutive) determinate, per ogni assunta composizione chimica, dall'unico parametro M = massa delle stelle. Si è qui assunto implicitamente che le fluttuazioni nei tempi della formazione stellare siano trascurabili rispetto ai tempi evolutivi. Lungo un isocrona è dunque L = L(M,t) Te=Te(M,t) al variare del parametro M. Con terminologia mutuata dall'idrodinamica diremo in definitiva che le tracce evolutive delle strutture costituiscono le linee di corrente del fluido stellare, mentre l'isocrona rappresenta la linea materiale del fluido all'istante t=t₀.


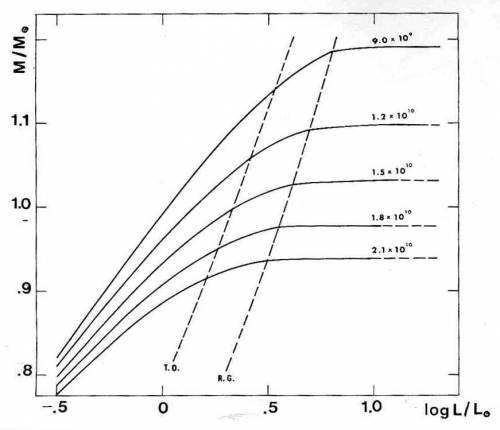
Fig. 6.24 La relazione massa-luminosità lungo isocrone teoriche per età comprese tra 9 e 21 miliardi di anni.

Si è già indicato come nelle fasi evolutive avanzate aumenti la velocità evolutiva, definibile attraverso il valore delle derivate $(\partial L/\partial t)_M$ e $(\partial T_e/\partial dt)_M$ che regolano la variazione con il tempo della posizione di una struttura nel diagramma HR. Si è anche intuitivamente indicato come in tali condizioni sia lecito confondere l'isocrona con la traccia evolutiva comune al ridotto intervallo di tracce evolventi.

Possiamo precisare le motivazioni e i limiti di una tale approssimazione definendo lungo una generica isocrona la variabile curvilinea S, cosi che S(M,t) risulti univocamente determinata e implicitamente resolubile rispetto a qualsivoglia delle variabili M,t. Dalla definizione di isocrona si ha allora:

$$ dt(M,S) = (\frac{\partial t}{\partial M})_S dM+ (\frac{\partial t}{\partial S})_M dS$$

da cui si ottiene per la variazione delle masse lungo l'isocrona

$$(\frac {\partial M}{\partial S})_t= - ( \frac {\partial M}{\partial t})_S (\frac {\partial t}{\partial S})_M $$

Si verifica cosi innanzitutto che per

$$(\frac {\partial S}{\partial t})_M \rightarrow \infty \ \ \ (\frac {\partial M}{\partial S})_t \rightarrow 0 $$

cioè che al crescere della velocità evolutiva $(\partial S/ \partial t)_M$ tende a zero la variazione di massa lungo l'isocrona.

L'osservazione fornisce non solo la collocazione nel diagramma HR della linea isocrona, ma anche il numero di stelle dN che popolano l'intervallo di ascissa curvilinea dS. Il dato osservativo $\Phi$=dN/dS è correlabile alle proprietà evolutive, risultando

$$\Phi(S,t_0) = \Psi(M) (\frac{\partial M}{\partial S})_t = -\Psi(M) (\frac{\partial M}{\partial t})_S(\frac{\partial t}{\partial S})_M $$

avendo indicato con $\Psi$(M) = dN/dM la distribuzione di masse propria dell'ammasso (IMF = Initial Mass Function). E' facile riconoscere che l'espressione precedente rappresenta semplicemente l'espressione euleriana dell'equazione di continuità. Per fasi evolutive avanzate, laddove tende a zero l'intervallo di masse popolanti l'isocrona, potremo porre $\Psi(M) \sim cost$ e cosi anche per il flusso temporale lungo l'isocrona ($\partial M/\partial t)_S \sim cost$. Se ne ricava che, sotto tali condizioni, il numero di stelle in una fase evolutiva avanzata risulta proporzionale al tempo speso dalle stelle evolventi lungo la loro traccia in tale fase.


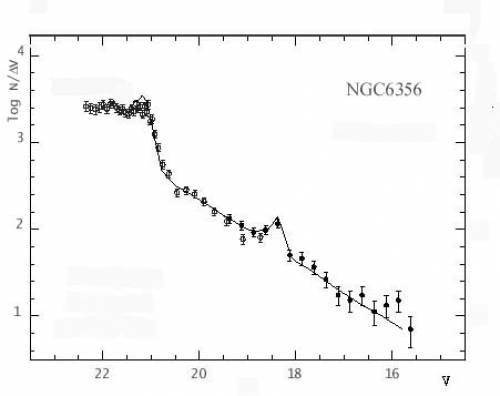
Fig. 6.25 Funzione di luminosità per l'Ammasso Globulare NGC6356 confrontata con le predizioni teoriche per la distribuzione dal Turn Off sino al tip del ramo delle giganti. I dati teorici assmono [Fe/H]=-0.9, età 14 Gyr, (m-M)v = 18.05.

Come utile applicazione di tale relazione abbiamo in precedenza discusso il caso della funzione di luminosità del ramo delle Giganti Rosse in un Ammasso Globulare. A titolo orientativo la Fig. 6.24 riporta la distribuzione teorica massa-luminosità lungo isocrone di età compresa tra 9 e 21 Gyr. Come atteso, la variazione della massa interessa essenzialmente le strutture di Sequenza Principale. Le subgiganti che si collocano tra il Turn Off e la base del ramo delle giganti hanno variazioni già più contenute, e dalla base delle giganti la massa evolvente diventa sensibilmente costante. Si è a suo tempo indicato come lungo il ramo delle giganti si possa porre

$$log\tau \propto logL \ \ \ {\rm dove} \ \ \ \tau = \frac{dt}{dlogL}$$

è la velocità evolutiva (in luminosità) delle giganti. Mostreremo qui che tale relazione è conseguenza diretta del fatto che lungo il ramo delle Giganti Rosse, come ogniqualvolta si sia in presenza di stelle con nucleo degenere, esiste una relazione massa del nucleo-luminosità

$$L = M_n^\alpha$$

che ci indica come in tali strutture sia la massa del nucleo degenere a governare la luminosità di una stella.

A fianco della precedente relazione potremo infatti considerare l'ulteriore relazione che collega la luminosità della struttura alla crescita temporale della massa del nucleo

$$ dM_n = \mu L dt $$

dove $\mu$ rappresenta la massa di elio sintetizzato nella produzione dell'unità di energia. Differenziando la prima relazione si ottiene

$$ dM_n =\frac{1}{\alpha}L^{\frac {1-\alpha}{\alpha}}dL $$ che sostituita nella seconda relazione conduce con facili passaggi a

$$\frac{dt}{dlogL} = \tau = \frac{1}{\mu \alpha}L^{\frac {1-\alpha}{\alpha}} $$

da cui la attesa relazione

$$log \tau = cost + \frac{1-\alpha}{\alpha}logL $$

La Fig.6.25 mostra come i riscontri sperimentali siano in generale in buon accordo con le previsioni, rivelando anche il bump delle giganti prodotto dall'incontro della shell di combustione di H con la discontinuità prodotta dall'affondamento della convezione superficiale.