7.6 Nane Bianche: la relazione massa-raggio
Per concludere il quadro evolutivo delle stelle di piccola massa resta da esaminare con ulteriori dettagli la configurazione delle strutture nella loro ultima fase di degenerazione elettronica. Da un punto di vista osservativo, la prima nana bianca venne alla luce dall'evidenza dell'esistenza di un “compagno oscuro” di Sirio, Sirio B. Dai parametri di tale sistema binario si ricavava per Sirio B una massa dell'ordine di 1 $M$_{\odot}$, con una luminosità pari a circa 1/500 di quella solare. Lo spettro, ottenuto nel 1915, rivelò peraltro una temperatura efficace dell'ordine di 9000 K. Dal bilancio tra emissività e luminosità (L=4$\pi$R$^2\sigma $T$_e^4$) si dovette necessariamente concludere per un raggio inferiore al 2% di quello solare e corrispondentemente, per densità dell'ordine almeno di 105 gr/cm3. In tali condizioni ci si attende una struttura elettronicamente degenere.
La struttura di una stella totalmente degenerata è retta dal
sistema politropico (–> 5.1 e A5.1):
$$\frac{dP}{dr} = - \frac{ GM_r \rho }{ r^2 }$$
$$\frac{dM_r}{dr} = 4 \pi r^2 \rho$$
$$P = k \rho^\gamma.$$
ove, a differenza del caso dei gas non degeneri, ambedue
gli indici k ed $\gamma$ sono univocamente determinati dalla
condizione di degenerazione elettronica. Nel caso di degenerazione
non-relativistica ($\rho < 10^6$ gr/cm$^3$) si ha:
$$P = 1.0 * 10^{12} (\rho/\mu_e)^ {5/3} $$
da cui una politropica di indice 3/2. Al crescere della
densità gli elettroni sono spinti a energie relativistiche. Al
limite relativistico (P$_e >$ m$_e c^2, \rho > 10^6 $ gr/cm$^3$)
risulta analogamente:
$$P = 1.2 * 10^{15} (\rho/\mu_e)^ {4/3} = {\rm politropica \ di \ indice \ 3} $$.
Dalla struttura del sistema politropico discende che per ogni
fissata densità centrale $\rho_c$ resta fissata la pressione
centrale e, con essa, tutta la struttura ed in particolare la
massa ed il raggio della stella. Ad ogni massa deve dunque
corrispondere una e una sola densità centrale ed un determinato
raggio della struttura degenere. Ciò è una conseguenza diretta
del fatto che, se tutta la pressione è fornita dagli elettroni
degeneri, pur se le temperature possono essere ancora elevate il
contributo dell'energia termica è trascurabile.
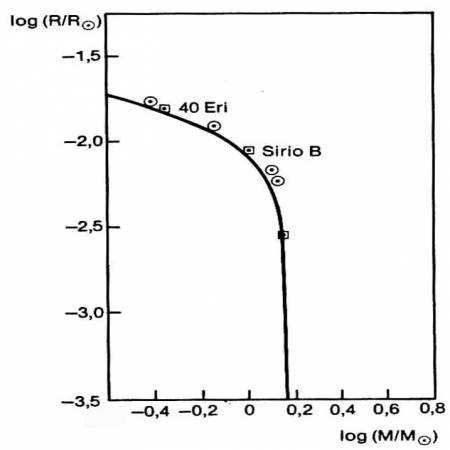
Fig.7.17 La relazione teorica massa-raggio per
strutture elettronicamente degeneri confrontata con i dati
sperimentali per alcune Nane Bianche.
Nel caso di degenerazione non relativistica, una semplice
valutazione di ordini di grandezza consente di valutare la
dipendenza di raggio e densità centrali dalla massa. Ponendo
infatti $\rho \sim M/R^3$, si ha dall'equilibrio idrostatico:
$$ P \sim \frac {GM^2}{R^4}$$
ma è anche $P=K\rho^{5/3} \sim K M^{5/3}/R^5$, da cui
$$ R \propto M^{-1/3} \ \ \ \rm e \ anche \ \ \ \rho \propto M^2$$
Maggiore è la massa della struttura minore deve dunque essere il
raggio della medesima. Ciò discende dal fatto che al crescere
della massa la densità centrale necessaria per sostenere la
struttura cresce col quadrato della massa stessa. La soluzione
della politropica fornisce in effetti per il raggio di una Nana
Bianca di M masse solari:
$$R \sim \frac{ 0.02 }{\mu_e^{5/3}M^{1/3}} \ \ \ R_{\odot}$$
dove $\mu_e$, peso molecolare medio per elettrone, è stato
già a suo tempo definito come la massa, in unità della massa
dell'idrogeno, per elettrone libero. Fatta eccezione per il caso
dell'idrogeno ($\mu_e$ = 1), che peraltro riveste scarsa
importanza nel quadro evolutivo che stiamo esaminando, per tutti
gli altri elementi si ha $\mu_e \sim $ 2, e, in particolare, si ha
$\mu_e$=2 per $^{4}$He, $^{12}$C, $^{16}$O, $^{20}$Ne. Il raggio di
una struttura degenere evoluta dipende quindi solo dalla massa, e
non dipende dalla composizione chimica della struttura stessa
nè, come si è più volte ripetuto, dal suo contenuto termico.
La relazione precedente resta valida per M $\le$ 0.5 M$_{\odot}$. Per masse superiori si raggiungono densità a cui interviene la degenerazione relativistica, che tende ad accrescere la dipendenza del raggio dalla massa. La Fig. 7.17 mostra come queste previsioni teoriche siano ben confortate dai dati sperimentali per alcune nane bianche appartenenti a sistemi binari, confortando, in ultima analisi, le correnti valutazioni teoriche sulle proprietà della materia degenere.
Un'indipendente indicazione osservativa sul rapporto M/R nelle
nane bianche è fornita dallo spostamento delle righe spettrali
(redshift) causato dal forte campo gravitazionale, in accordo con
le prescrizioni della relatività generale. Per un fotone di
energia h$\nu_0$ emesso alla superficie di una stella di massa M e
raggio R, che raggiunga un osservatore all'infinito potremo
infatti porre
$$h\nu = h\nu_0 - \frac {GM}{R}\frac {h\nu_0}{c^2}$$
dove il secondo termine al secondo membro rappresenta il
lavoro del campo gravitazionale delle stella. Se ne ricava
immediatamente
$$\frac{\nu_0 - \nu}{\nu_0}= \frac {GM}{Rc^2}$$
Tale redshift, trascurabile in strutture stellari normali, diviene
oservabile nelle nane bianche a causa della grande gravità superficiale.
Viene sovente riportato sotto forma di Effetto Doppler
Equivalente ponendo $\Delta \lambda/\lambda = v/c$, da cui
$$v=0.64 \frac {M}{R} \ \ \ {\rm km/sec}$$
dove M e R sono in unità solari. Per le due Nane Bianche Sirio B
e Keid B (chiamate rispettivamente “CMa B” e “40 Eri B” nella Nomenclatura di Flamsteed) si ottiene così v = 92 ± 8 km/sec e 22 ± 1.4 km/sec.
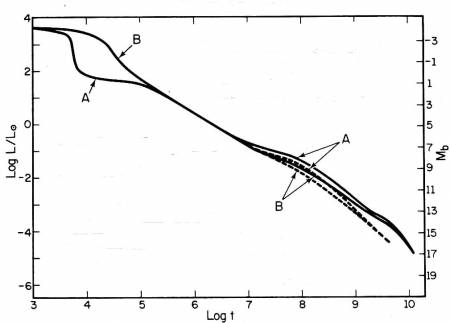
Fig. 7.18 Andamento con il tempo della luminosità
di un modello di Nana Bianca di CO, 0.6 M$_{\odot}$. Nelle linee
a tratti è trascurato il calore di cristallizzazione. Caso A:
inviluppo di 1.5 10$^{-4}$ M$_{\odot}$ di H; caso B: inviluppo di
0.016 M$_{\odot}$ di He. Il tempo t è in anni.
Da un punto di vista generale, asserire che per ogni prefissata
massa una Nana Bianca ha un raggio fissato, indipendentemente da
ogni assunzione su temperatura e luminosità, significa indicare
che la Nana si comporta come un corpo solido, quali - per fornire
un'immagine- una sfera di metallo o un mattone. Tale corpo,
formatosi da materia ad altissime temperatura, perderà energia
irraggiando dalla sua superficie come un corpo nero, a spese
dell'energia degli ioni, essendo ormai gli elettroni nel loro
stato di minima energia compatibile con la loro natura di
fermioni. La struttura percorrerà quindi nel diagramma HR una
sequenza a raggio costante (L $\propto$ T$_e^4$) dissipando prima
l'energia di agitazione termica degli ioni e poi anche il calore
di cristallizazione degli stessi, destinata a raffreddarsi sino a
porsi in equilibrio con il fondo cosmico dell'Universo o, più in
generale, con il campo di radiazione locale.
All'inizio del raffreddamento la velocità con la quale decresce la luminosità è molto alta, perchè corrispondentemente alte sono le perdite per irraggiamento. Al diminuire della luminosità decresce anche la temperatura efficace e con questa diminuiscono anche le perdite di energia, e i tempi evolutivi si allungano corrispondentemente. La Fig. 7.18 riporta un esempio dell'andamento temporale della luminosità di un modello di Nana Bianca lungo la sua sequenza di raffreddamento, mostrando il rallentamento portato dal contributo del calore di cristallizzazione. Si noti come i tempi di raffreddamento dipendono anche dalle dimensioni e dalla composizione di sia pur tenui inviluppi residui, sia per il possibile contributo energetico di combustioni superficiali di idrogeno, sia perchè l'opacità degli inviluppi governa la temperatura efficace e, quindi, le perdite di energie della struttura.
La figura mostra come i tempi di raffreddamento possano
raggiungere e superare i 1010 anni: ci si attende di
conseguenza che anche negli ammassi stellari più antichi, quali
gli ammassi globulari, le prime Nane formatesi non abbiano ancora
terminato il loro raffreddamento, marcando quindi con la loro
luminosità il tempo della loro formazione. La
Fig. 7.19 mostra la l'andamento nel diagramma HR di
sequenze di egual raggio calcolate per varie masse, poste a
confronto con la distribuzione osservata per un campione di Nane
Bianche di campo.
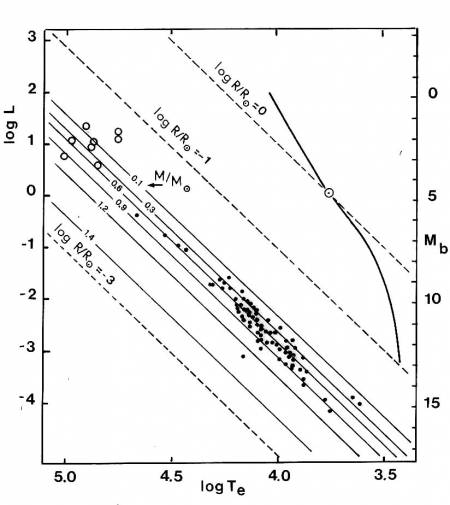
Fig. 7.19 Sequenze teoriche di raffreddamento di
Nane Bianche ($\mu_e = 2$) per vari valori della massa. Per
confronto sono riportate alcune linee R=cost ed è indicata la
collocazione di una Sequenza Principale. I cerchietti aperti
mostrano la collocazione di alcuni nuclei di Nebulosa Planetaria,
progenitori di Nane Bianche a minor temperatura efficace.
Per concludere ricordiamo come le densità in una Nana Bianca restino fissata una volta fissata massa e $\mu_e$. Il numero di particelle per unità di volume sarà peraltro inversamente proporzionale alla massa delle medesime. Poichè ogni ione possiede una energia $\propto$ kT, ne segue, ad esempio, che una Nana Bianca di He avrà - a parità di temperature - un contenuto termico molto maggiore di una Nana di CO e, corrispondentemente, tempi di raffreddamento più lunghi.
