7.7 La massa limite di Chandrasekhar
La teoria pone un limite superiore alla massa di una struttura sorretta dalla degenerazione elettronica, pari a circa 1.4 M$_{\odot}$. Tale limite (limite di Chandrasekhar) fu a suo tempo ricavato come conseguenza diretta delle relazioni fisiche che siamo andati sin qui esponendo. Si può comprendere l'origine di tale limite ricordando che al crescere della massa cresce la densità (serve maggior pressione degli elettroni) e la degenerazione è fatalmente spinta verso il regime relativistico.
Al limite pienamente relativistico esiste una ed una sola
struttura possibile, la cui massa è fornita dalla relazione
$$ M = \frac {5.75}{\mu_e^2} M_{\odot}$$
Ripetendo il precedente calcolo di ordini di grandezza nel caso
relativistico (P $\propto \rho^{4/3}$) si ha infatti:
$$P \sim \frac{G M^2}{R^4} \ \ \ {\rm e \ \ anche} \ \ \ P \sim \frac
{K M^{4/3}}{R^4}$$
da cui si ricava la massa M = (K/G)$^{-2/3}$. In pratica
si trova che raggiungendo la piena degenerazione relativistica la
struttura dovrebbe ridursi ad un punto, né sono permesse
strutture di equilibrio con masse maggiori.
Al di là di tale approccio analitico, il problema della massa
limite è in realtà governato da meccanismi fisici più
complessi. Al crescere della densità cresce l'energia raggiunta
dagli elettroni, finendo col superare la soglia per reazioni
<tex>$\beta$</tex> inverse sui nuclei. Quando infatti l'energia di un
elettrone diviene superiore all'energia del decadimento <tex>$\beta$</tex> di
un nucleo di numero di massa A e carica Z-1, diventano possibili
le reazioni
$$e^- + (Z,A) \rightarrow (Z-1,A) + \nu $$
La Tabella 4 riporta le densità di soglia per
l'innesco di tali processi per diverse specie atomiche.
| Reazione | Energia (MeV) | $\rho_0 (gr * cm^{-3})$ |
|---|---|---|
| $ ^1_1H \rightarrow n$ | 0.782 | 1.22*10$^7$ |
| $ ^4_2He \rightarrow ^3_1H + n \rightarrow 4n$ | 20.596 | 1.37*10$^{11}$ |
| $^{12}_{~6}C \rightarrow ^{12}_{~5}B \rightarrow ^{12}_{~4}Be$ | 13.370 | 3.90*10$^{10}$ |
| $^{16}_{~8}O \rightarrow ^{16}_{~7}N \rightarrow ^{16}_{~6}C$ | 10.419 | 1.90*10$^{10}$ |
| $^{20}_{10}Ne \rightarrow ^{20}_{~9}F \rightarrow ^{20}_{~8}O$ | 7.026 | 6.21*10$^{9}$ |
| $^{24}_{12}Mg \rightarrow ^{24}_{11}Na \rightarrow ^{24}_{10}Ne$ | 5.513 | 3.16*10$^{9}$ |
| $^{28}_{14}Si \rightarrow ^{28}_{13}Al \rightarrow ^{28}_{12}Mg $ | 4.643 | 1.97*10$^{9}$ |
| $^{32}_{16}S \rightarrow ^{32}_{15}P \rightarrow ^{32}_{14}Si$ | 1.710 | 1.47*10$^{8}$ |
| $^{56}_{26}Fe \rightarrow ^{56}_{25}Mn \rightarrow ^{56}_{24}Cr$ | 3.695 | 1.14*10$^{9}$ |
Tabella 4 Densità di soglia per la neutronizzazione. Dall'energia
di soglia è sottratta l'energia di massa dell'elettrone
mec2 =0.511 MeV.
Valutazioni dettagliate (Fig. 7.20) mostrano che che al
crescere della massa di una struttura elettronicamente degenere, e
quindi della sua densità, avvicinandosi alla massa limite di
Chandrasekhar intervengono processi $\beta$ inversi che,
aumentando $\mu_e$, inducono una diminuzione della massa limite.
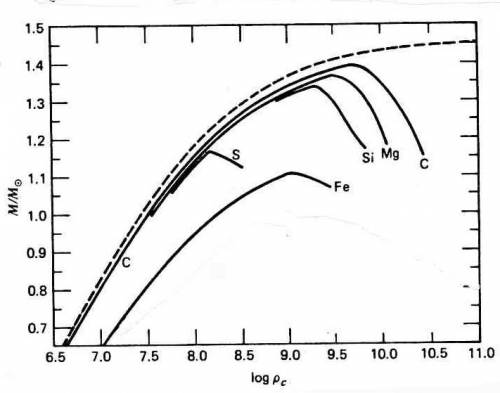
Fig.7.20 Relazioni massa-densità centrale per
strutture elettronicamente degeneri di varia composizione, tenendo
in conto i processi $\beta inversi. La linea a tratti mostra la
soluzione di Chandrasekhar per $\mu_e$ = 2.
La Fig. 7.21 riporta una sintesi generale di tali
risultati. Alle densità minori si trova il campo di esistenza
delle strutture elettronicamente degeneri sin qui discusse. Al
crescere ulteriore della densità centrale si hanno strutture
instabili in cui la massa decresce all'aumentare di $\rho_c$. Si
ritrova una zona di stabilità solo a densità dell'ordine di
$\rho_c \sim $10$^{14}$ - 10$^{16}$ per strutture sorrette ora da
neutroni degeneri (Stelle di neutroni). I neutroni, con spin
1/2, sono infatti anch'essi fermioni che ubbidiscono alla
statistica di Fermi Dirac, in grado quindi di sviluppare una
pressione di degenerazione. Nel caso non relativistico si trova
così P $\sim$ 4 10$^{9} \rho^{5/3}$. A titolo orientativo
ricordiamo qui che il raggio tipico di una stella di neutroni
risulta dell'ordine di 10 km, contro i 103-104 km di una
Nana Bianca e i 106 km del Sole.
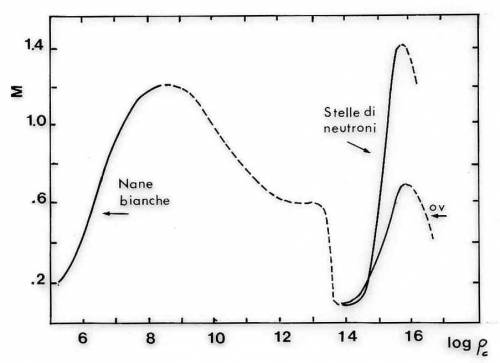
Fig.7.21 Relazioni massa-densità centrale per
strutture sorrette da elettroni o neutroni degeneri. Le linee a
tratti rappresentano strutture instabili. Per le stelle di
neutroni è riportata la soluzione ricavata dall'equazione di
Oppenheimer-Volkoff (OV) assieme ad una soluzione che include
opportune interazioni tra neutroni.
Alle densità delle stelle di neutroni non è peraltro più
valida l'approssimazione Newtoniana, e il campo gravitazionale
dovrà essere descritto in accordo con la relatività generale,
secondo l'equazione di Oppenheimer Volkoff (–> A2.3).
La soluzione dipende dalle assunzioni che devono essere
necessariamente fatte sull'equazione di stato della materia
neutronica. Si ritrova in ogni caso ancora una massa limite, ma il
valore di tale massa dipende criticamente da tali assunzioni.
Assumendo l'equazione di stato non relativistica si troverebbe una
massa limite M $\sim$ 0.7 M$_{\odot}$. La figura 7.21
mostra peraltro un esempio di come equazioni di stato che
introducono opportunele interazioni tra neutroni possano innalzare
la massa limite per tali strutture. Oggi si ritiene che il limite
di massa per le stelle a neutroni si collochi attorno alle 2 - 3
$M_{\odot}$, anche se la maggioranza delle stelle di neutroni
osservate come pulsar ha masse attorno alle 1.4 M$_{\odot}$.
A titolo orientativo ricordiamo qui che il raggio tipico di una
stella di neutroni risulta dell'ordine di 10 km, contro i
103-104 km di una Nana Bianca
e i 106 km del Sole. Per le
Nane Bianche resta in ogni caso stabilito un limite superiore di
massa dato, con buona approssimazione, dal limite di Chandrasekhar
M$_{Ch}$ precedentemente riportato. Per una struttura di idrogeno
$\mu_e$=1 e M$_{Ch}$ = 5.8 M$_{\odot}$, un limite di scarsa
rilevanza perchè sappiamo che in condizioni normali strutture di
H di massa maggiore di 0.1 M$_{\odot}$ giungono ad innescare la
combustione dell'idrogeno. Per 4He, 12C,
16O, 20Ne etc $\mu_e = 2$ e quindi
$M_{Ch}\ \ \sim \ 1.4 M_{\odot}$
limite che giocherà un ruolo essenziale nell'evoluzione delle
stelle massicce e nella produzione di Supernovae di tipo I nei
sistemi binari.
Per completezza, ricordiamo infine che a temperatura zero ma densità sufficientemente alte diventano possibili anche reazioni nucleari: l'energia dei nuclei nel lattice può divenire sufficientemente elevata da superare la repulsione coulombiana, dando luogo a reazioni che prendono il nome di reazioni picnonucleari, dal greco “pyknos” = denso. Si stima che a 106 gr cm-3 H sarebbe convertito in He in circa 105 anni, e a 1010 gr cm-3 He sarebbe convertito in C. Il calcolo di tali processi è peraltro molto difficoltoso, e i valori riportati sono solo indicativi.
