A10.2 Curve di luce e curve di velocità.
La Fig. 10.12 riporta le curve di luce sperimentali
per la variabile RR Lyrae nelle bande U, B e V di Johnson. E'
facile riconoscere come l'ampiezza della curva di luce dipenda
dala banda, raggiungendo un massimo per la banda B. La ragione di
tale comportamento è subito compresa quando si esamini
l'andamento temporale dell'indice di colore B-V.
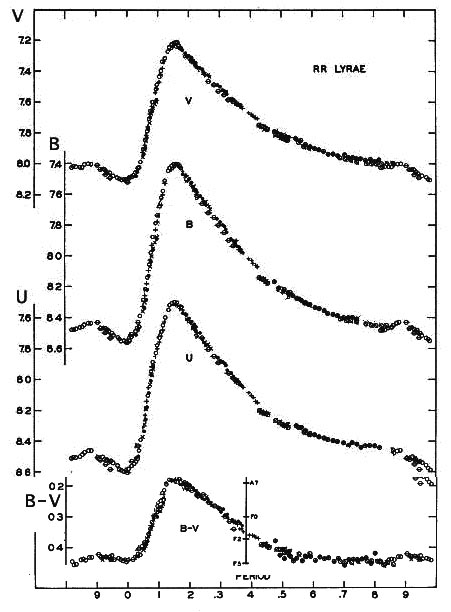
Fig. 10.12 Curve di luce nella bande U, B, V della
variabile RR Lyrae. In basso è mostrato l'andamento temporale
dell'indice di colore B-V.
Si vede come al
minimo in luminosità corrisponda un massimo del colore
(B-V$\sim$0.4) e quindi un minimo della temperatura. Analogamente,
al massimo di luminosità corrisponde il minimo di B-V e un
massimo della temperatura. Alla variazione della luminosità
bolometrica (= totale) della struttura si sovrappone quindi un
effetto di temperatura che aggiunge radiazione nella banda B in
prossimità del massimo e toglie radiazione, spostandola a
maggiori lunghezze d'onda, in prossimità del minimo. Se ne
conclude che l'aumento di emissività collegato all'aumento di
temperatura efficace giuca un ruolo importante nella curva di
luce.
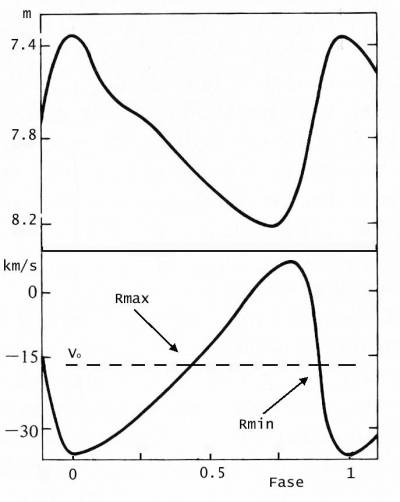
Fig. 10.13 Curva di luce e andamento delle velocità
radiali tipiche di pulsatori radiali, quali RR Lyrae e Cefeidi.
Ulteriori ed importanti informazioni sono fornite dalla curva di
velocità radiale, ricavabile dall'effetto Doppler sulle righe
spettrali. La Fig. 10.13 mostra come tutti i pulsatori
radiali presentino curve di velocità caratteristicamente
speculari rispetto alla curva di luce. Le velocità misurate V
risultano dalla combinazione della velocità della pulsazione
V$_r$ alla velocità radiale V$_0$ intrinseca all'oggetto
pulsante. Quest'ultima è peraltro ricavabile dalla ovvia
condizione che l'integrale rispetto al tempo della velocità
radiale propria della pulsazione , che rappresenta in ogni istante
lo spazio in km di cui si è spostata la fotosfera stellare,
debba annullarsi quando esteso ad un ciclo
$$ \int (V-V_0) \ dt \ = \ 0$$
Si ottiene così agevolmente il valore di V$_0$, rappresentato
in Fig. 10.13 dalla linea che divide la curva delle
velocità in due porzioni che, per definizione, sottendono eguali
aree. Dai dati nella stessa figura è ora facile verificare che
il massimo di luminosità cade in un punto intermedio della fase
di espansione, in corrispondenza del massimo in temperatura
efficace. Il successivo aumento di raggio è controbilanciato
dalla diminuzione di temperatura che porta, in totale, ad una
diminuzione della luminosità.
Quando si voglia risalire dalle velocità radiali osservate alla
cinematica della pulsazione occorre tener presente che il dato
osservativo fa riferimento alla media sull'emisfero stellare
visibile della componente della velocità nella direzione
dell'osservatore, componente che è in genere minore della reale
velocità radiale, ed uguale ad essa solo nel punto centrale
dell'emisfero osservato. La misura sperimentale fornisce quindi un
valore inferiore del vero valore della velocità radiale. Con
semplice calcolo si trova per altro che sussiste la
proporzionalità
$$ V_r (misurata) = 2/3 V_r (reale)$$
Dalle curve di luce nelle varie bande si ottengono infine le
corrispondenti magnitudini medie come integrali sull'intero ciclo
del segnale raccolto. Al riguardo sono peraltro utilizzate in
letteratura due alternative opzioni, consistenti in
- Medie in magnitudine: (U), (B), (V) –> ricavate per ogni banda come media temporale delle magnitudini istantanee
- Medie in intensità: $\langle$U$\rangle$, $\langle$B$\rangle$, $\langle$V$\rangle$ … –> ricavate dal logaritmo della media temporale dei flussi energetici.
Poichè la media del logaritmo non è il logaritmo della media le due grandezza differiscono, anche se non di molto, tra loro. Dalle singole magnitudini medie si ricavano così i colori medi in magnitudine (B-V) o in intensità $\langle$B-V$\rangle$. In letteratura è stato a lungo dibattuto il problema di quale tra questi due colori approssimi meglio il colore della struttura statica. In realtà è stato infine mostrato che ambedue questi colori osservativi tendono a discostarsi dal colore della struttura statica quanto più la curva di luce risulta asimmetrica.
Esistono al riguardo opportune correzioni che consentono di
risalire dai colori medi osservati ai colori statici, passaggio
obbligato quando si vogliano inserire i risultati osservativi per
le variabili nel contesto delle teorie evolutive e dei loro colori
statici. La Fig. 10.14 mostra come esempio il
confronto tra colori B-V in magnitudine o in intensità per un
campione di RR Lyrae nell'ammasso globulare M5, senza o con
correzione per colore statico.
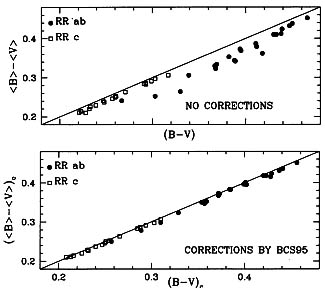
Fig. 10.14 Confronto tra colori B-V in magnitudine o
in intensità per un campione di RR Lyrae nell'Ammasso Globulare
M5, senza o con correzione al colore statico.
