L'osservazione infrarossa di campioni di RR Lyrae in Ammassi Globulari galattici ha portato alla luce una serie di interessanti caratteristiche che hanno stimolato un crescente uso delle magnitudini nella banda K, che copre l'intervallo di lunghezze d'onda 2.0-2.5 micrometri. Nel seguito faremo riferimento a tale problematica, avvisando peraltro che quanto andremo esponendo trova del tutto analoghe applicazioni anche nel campo delle variabili Cefeidi.

Una prima caratteristica è che in tale banda l'ampiezza delle curve di luce risulta estremamente ridotta, e le magnitudini medie corrispondono senza ambiguità alle magnitudini statiche. Molto più importante è l'osservazione che in tale banda si manifesta una relazione Periodo-Magnitudine che, osservativamente, pare non dipendere dalla metallicità degli ammassi e, quindi, dal preciso livello di luminosità del Ramo Orizzontale. La teoria predice infatti che tale luminosità debba leggermente decrescere al crescere della metallicità, diminuendo di circa $\Delta$logL $\sim$ 0.07 ($\Delta$ M $\sim$ 0.17 mag) passando da Z=0.0001 a Z=0.001.

L'indagine teorica dà ragione di un tale accadimento, fornendone una semplice chiave interpretativa. Per illustrare il differente comportamento nelle varie bande la Fig. 10.15 riporta nel pannello superiore l'attesa distribuzione di periodi per strutture distribuite lungo la strip a tre assunte diversi livelli di luminosità. Come atteso, le magnitudini visuali seguono i livelli di luminosità, con solo leggere variazioni collegate anche a piccole variazioni della correzione bolometrica e alla differenza tra magnitudini medie e magnitudini statiche. Questo perché la quantità di radiazione raccolta dalla banda V dipende solo debolmente dalla temperatura delle strutture, temperatura che -per ogni prefissato livello di luminosità- va decrescendo dai periodi minori (FOBE) verso il massimo periodo, raggiunto al FRE.

Il pannello inferiore della stessa figura mostra la distribuzione delle medesime strutture nella banda K. Facendo riferimento ad un qualunque livello di luminosità, ora si nota che al diminuire della temperatura aumenta sensibilmente la radiazione raccolta dalla banda K e. conseguentemente, per ogni prefissato livello di luminosità si genera una relazione Periodo-Magnitudine K. Inoltre, l'esistenza di una tale relazione fa anche sì che all'aumentare del livello di luminosità, il corrispondente aumento del periodo riporta il punto del piano $logP-Mk$ verso la relazione caratteristica delle minori luminosità. La conseguenza è che nel piano $logP-Mv$, un'incertezza $\pm$ 0.1 in logL, per ogni prefissato periodo si traduce in un incertezza di $\sim$ 0.25 mag in Mv. Dal pannello inferiore della Fig. 10.15 si ricava che nel piano $logP-Mk$ la stessa incertezza sul livello di luminosità bolometrica delle strutture pulsanti si traduce in un incertezza di $\sim$0.07 mag su Mk.


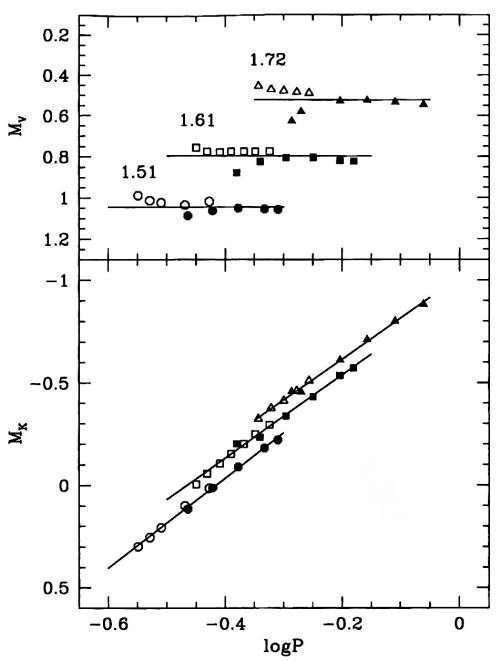
Fig. 10.15 Pannello superiore: La distribuzione nel piano $logP-Mv$ di strutture di HB distribuite lungo la strip ai tre indicati livelli di luminosità . Pannello inferiore: Come nel pannello superiore ma per il piano $logP-Mk$

Se ne trae che anche accettando un'incertezza $\Delta$logL = 0.1 sulle valutazioni teoriche della luminosità dei Rami Orizzontali, quindi ben superiore a quanto oggi si ritenga ($\Delta$ logL$\sim \pm$ 0.03), l'osservazione in banda K delle RR Lyrae consente di fissare il modulo di distanza di un ammasso entro $\pm$ 0.07 mag. Per ciò che riguarda l'effetto di metallicità è immediato ricavare che una variazione di $\Delta$logL = 0.07 si traduce nel piano $logP-Mk$ in una dispersione delle magnitudini K pari a $\pm$0.025 mag, confortando di fatto la pratica indipendenza dalla metallicità.

L'adozione della banda K agisce quindi nel senso di rompere la degenerazione tra periodi e magnitudini, associando ad ogni periodo solo un ristretto intervallo di magnitudini. Analogo effetto ha, peraltro per tutt'altri motivi, l'adozione degli indici “reddening free” definiti a suo tempo da Wesenheit come utili parametri osservativi indipendenti dall'arrossamento interstellare. Ricordando, ad esempio, che per l'estinzione nella banda V sussiste la relazione

$$ A_V = 3.10 E(B-V)$$

si riconosce che per la funzione di Wesenheit $$W(B,V) = V-3.1(B-V)= V_0-3.10(B-V)_0$$

E' infatti

$$V-3.10(B-V)= V_0 +A_v -3.10(B-V)_0 -3.10E(B-V) $$

da cui si ha subito il precedente enunciato. Indici di Wesenheit possono essere definiti per qualunque coppia di bande fotometriche e, ad esempio, per le bande V,I si ha

$$W(V,I) = V-2.54E(V-I)$$

Questa volta la degenerazione viene rotta perché per una popolazione di pulsatori che riempia la strip a V$\sim$ cost W decresce al crescere di (B-V) dal FOBE al FRE, creando una relazione logP(W). Si hanno in definitiva risultati del tutto analoghi a quelli discussi per la banda K, con quindi analoghe applicazioni osservative.