11.2 Processi di neutronizzazione lenta (S)
Le temperature di fotodisintegrazione del Fe sono le massime
raggiungibili all'interno di una struttura stellare e i nuclei
del picco del Fe sono di conseguenza i più complessi prodotti
delle reazioni termonucleari. I nuclei oltre il Fe possono quindi
ben difficilmente essere prodotti da reazioni nucleari tra
particelle cariche, che richiederebbero temperature ancor maggiori
di quelle raggiungibili nelle stelle. Per rendere ragione della
presenza in natura di tali elementi e, nel contempo, per
rispettare i limiti di temperatura imposti dalle stelle dovremo
considerare reazioni nucleari non regolate dalla repulsione
colombiana, invocando quindi la presenza di neutroni.
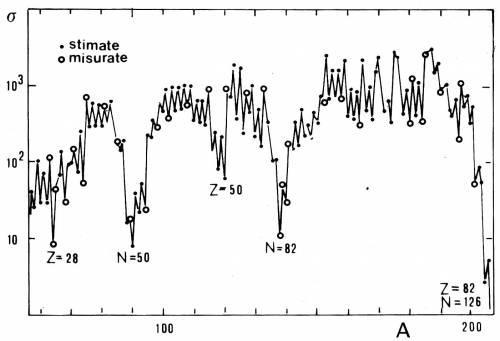
Fig. 11.3 Sezione d'urto per cattura neutronica
indunzione del numero atomico . E' evidente la forte diminuzione
in corrispondenza dei numeri magici. Si noti anche l'effetto
pari-dispari. La sezione d'urto è in mb (1 b= 1 barn =
10-24 cm2) per neutroni di 25 keV
Vi sono peraltro in natura chiari indizi che supportano
l'efficienza di processi di cattura neutronica. In Fig. 11.1
si può notare come la distribuzione degli
elementi “transferrici” sia modulata da una serie di
caratteristiche ricorrenze, tra le quali la presenza dei picchi di
abbondanza contrassegnati dalla lettera “S”. Tali picchi
corrispondono con precisione ai cosiddetti nuclei “magici”, nuclei
che in corrispondenza di determinati numeri “magici” di neutroni o
protoni (N= 2, 8, 20, 28, 50, 82, 126) mostrano particolari doti
di stabilità (–> A1.8). In un modello a shell del
nucleo a tali numeri corrisponderebbe il completamento di una
shell, e la stabilità dei corrisponedenti nuclei sarebbe
l'analogo della stabilità mostrata dagli atomi dei gas nobili.
Come mostrato in Fig. 11.3, quel che qui ci interessa
è che a tali nuclei corrisponde un brusca diminuzione della
sezione d'urto per cattura neutronica. La correlazione tra
abbondanze in natura e sezioni d'urto per cattura neutronica rende
plausibile la supposta efficienza di tali processi e, come
vedremo, renderà ragione della anomale abbondanze dei picchi “S”.
Il neutrone è peraltro particella instabile, che decade in un protone (più e$^+ \nu$) con tempo di dimezzamento di circa 15 minuti(–> A1.10). Perchè il processo possa essere efficiente dobbiamo quindi richiedere non solo una sorgente di neutroni, ma anche che tale sorgente sia immersa in materia sufficientemente densa perchè i neutroni possano interagire prima di decadere. Tali condizioni sono spontaneamente realizzate ancora all'interno delle stelle, dove abbiamo visto che durante la combustione di elio diventa efficiente la produzione dei neutroni tramite la catena dell' $^{14}$N. Le stelle si presentano dunque spontaneamente come luoghi in cui, a fianco delle reazioni termonucleari, devono diventare efficienti processi di cattura neitronica che, pur non contribuendo all'energetica della stella, pssono portare un contributo sostanziale alla nucleosintesi degli elementi pesanti.
Poichè la considerazione o meno di tali processi non influisce
sull'evoluzione delle strutture, le valutazioni dell'efficienza
dei processi stessi viene sovente eseguita sulla base di una
sequenza di strutture evolutive opportunamente memorizzzate. Se ne
ricava l'evidenza che i neutroni prodotti dalla catena dell'
$^{14}$N possono venir catturati da preesistenti nuclei di
elementi pesanti (Nuclei “seme”), nuclei che a seguito di
una serie di tali catture neutroniche si spostano progressivamente
lungo la valle di stabilità (–> ….) andando a
formare gli elementi oltre il Ferro.
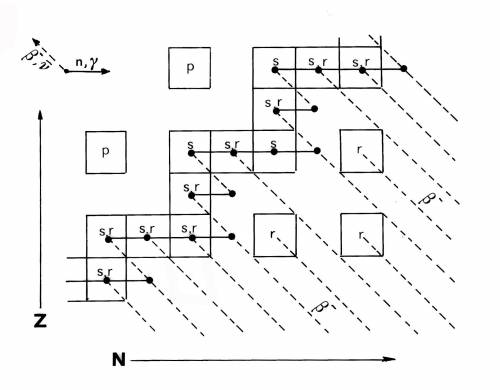
Fig. 11.4 Esemplificazione della tipica traiettoria
dei processi S nel piano N (numero di neutroni) Z (numero di
protoni). Le “isole” sulla sinistra della valle di stabilità
schermano i nuclei della stessa dal contributo dei processi r. I
nuclei possono cosi essere distinti in r-puri ('r'), S-puri ('S') o
do origine mista ('S,r').
Nel caso della combustione dell'H avevamo già visto come una
serie di catture protoniche su nuclei stabili finisca
inevitabilmente col produrre elementi instabili per eccesso di
protoni, nuclei che vengono richiamati sulla valle di stabilità da
decadimenti $\beta^+$. Ora una serie di catture neutroniche
finisce inevitabilmente col produrre elementi instabili per
eccesso di neutroni, che vengono richiamati sulla valle di
stabilità da decadimenti $\beta^-$. Poichè i neutroni vengono
prodotti su tempi scala termonucleari, il loro flusso rimane
contenuto e si può assumere che il processo sia “lento”
(S = Slow) nel senso che il tempo tra due successive catture
neutroniche sia in ogni caso maggiore dei tempi di decadimento
degli elementi instabili $\beta^-$ prodotti. Cioè che i nuclei
instabili abbiano il tempo di decadere prima di catturare un
ulteriore neutrone.
Nel piano N,Z ne segue la caratteristica traiettoria illustrata in Fig. 11.4, tramite la quale i nuclei seme vengono spinti lungo la valle di stabilità a numeri atomici A sempre più alti. Notiamo peraltro subito che una traiettoria “S” non può raggiungere i nuclei stabili (le isole) separati, sia a destra come a sinistra, dalla sequenza centrale. Poichè tali nuclei sono presenti in natura, per essi dunque dovremo investigare diversi meccanismi di produzione.
Per ciò che riguarda i processi S, motiamo che ogni nucleo lumgo
la traiettoria si presenta come elemento “secondario”, nel senso
che ogni nucleo risulta prodotto da una cattura neutronica e
distrutto dalla successiva cattura. Se n è il numero di neutroni
nell'unità di volume e V la loro velocità, potremo dunque
scrivere per il generico nucleo di numero atomico A nell'unità
di tempo
$$ Produzione: \ \ \ dN_A = nN_{A-1}\sigma_{A-1}V$$
$$ Distruzione: \ \ \ dN_A = nN_{A}\sigma_{A}V$$
e, come ogni elemento secondario, il nucleo deve evolvere verso
una situazione di equilibrio nella quale in totale dN$_A$=0 e
quindi
$$N_{A-1}\sigma_{A-1}=N_{A}\sigma_{A} \ \ {\rm o \ anche, \ per \ ogni \ A} \ \ \ N_A \sigma_A = cost $$
Si vede subito come ad una sezione d'urto di cattura neutronica
$\sigma_A$ peculiarmente bassa, quale quella che caratterizza i
nuclei magici, debba corrispondere una abbondanza N$_A$
peculiarmente elevata, dando ragione dei picchi S osservati in
natura. Al limite, a sezioni d'urto nulle corrisponde una
indefinita crescita di abbondanza del nucleo A.
Notiamo infine come, a fianco della catena dell'$^{14}$N e al
molto minor contributo proveniente da reazioni più avanzate,
quali
$$^{16}O + ^{16}O \rightarrow ^{31}S + n$$
siano state suggerite anche altre possibili fonti di neutroni. In
particolare, nel caso di rimescolamento parziale di una zona in
combustione di He con strati ancora ricchi di idrogeno, i protoni
si combineranno con il Carbonio, come avviene nel ciclo CNO
$$ ^{12}C + p \rightarrow ^{13}N + \gamma$$
$$ ^{13}N \rightarrow ^{13}C + e^+ + \nu $$
Una successiva cattura protonica è però inibita dalla
scarsità di protoni, e segit\`a invece
$$^{13}C + \alpha \rightarrow (^{17}O)^* \rightarrow ^{16}O + n$$
che potrebbe risultare una notevolissima fonte di neutroni da
affiancare a quelli prodotti dalla catena dell'$^{14}N$.
