A2.3 L'equazione di Oppenheimer-Volkoff. Il raggio di Schwarzschild.
La formulazione newtoniana della gravitazione, così come
inserita nella relazione dell'equilibrio idrostatico, non può
essere mantenuta per campi gravitazionali estremi, quando
l'energia gravitazionale delle particelle diventa non trascurabile
a confronto dell'energia di massa $E = mc^2$.
Occorre in tal caso
ricorrere al formalismo della relatività generale. Adottando la
metrica di Schwarzschild, che governa il campo gravitazionale a
simmetria sferica generato da una massa “m”
$$ds^2 = - (1 -{r_g \over r}) d(ct)^2 + {1 \over {1 - r_g/r}} dr^2
+r^2(d\theta^2 +sin^2\theta d\Phi ^2)$$
dove
$$r_g = {2Gm \over c^2}$$
si giunge a riscrivere l'equazione dell'equilibrio idrostatico e
quella della conservazione della massa nella forma generalizzata
relativistica
$$\frac {dP}{dr}=-\frac {GM_r}{r^2} \rho
(1 + \frac {P}{\rho c^2}) (1 + \frac {4 \pi r^3 P}{M_r c^2})
(1 - \frac {2GM_r}{rc^2})^{-1}$$
$$\frac {dM_r}{dr}= 4 \pi r^2 \rho$$
dove $M_r$, massa contenuta all'interno del raggio “r”.
contiene il contributo non solo della massa a riposo delle
particelle ma anche quello della loro energia.
Le strutture in cui
si rende necessaria l'applicazione di un tale formalismo si
collocano in qualche maniera ai due estremi delle normali
strutture stellari: stelle supermassive e stelle di neutroni.
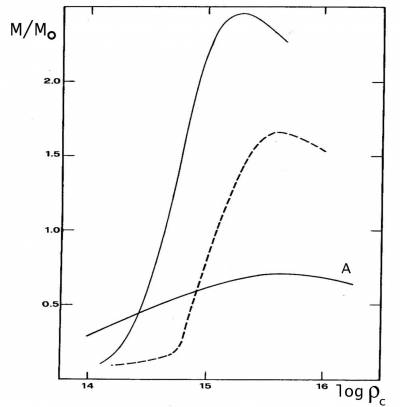
Figura 2.8 La relazione massa densità centrale per
le strutture di stelle di neutroni, La curva A indica la soluzione
per un gas di neutroni liberi mentre le altre curve portano esempi
di equazioni di stato più elaborate.
Per ciò che riguarda gli oggetti supermassivi ($M\sim 10^5-10^8
M_\odot $) è da notare che per i normali oggetti stellari esiste
un limite superiore, a poco più di 100 $M_\odot$, per la
formazione di strutture stabili. Ciò perchè al crescere della
massa il crescente contributo della pressione di radiazione
finisce col destabilizzare la stella. Al livello di
supermassività indicato intervengono però due nuovi fattori
che consentono, almeno in linea di principio, strutture
gravitazionalmente legate. Infatti il campo gravitazionale
efficace è enormemente accresciuto dall'equivalente in massa
dell'energia e, nel contempo, i fotoni perdono energia nel
propagarsi contro il campo gravitazionale, riducendo di molto gli
effetti della pressione di radiazione.
Oggetti supermassivi sono stati nel passato invocati per giustificare l'emissione luminosa da nuclei galattici, radiosorgenti e quasar. Per quanto tale ipotesi sia stata ormai abbandonata, è da notare che da una struttura di $10^5 M_\odot$ nelle fasi iniziali di combustione di idrogeno si attendono $\sim 10^{43}$ erg/sec, con temperature efficaci $(\rightarrow 1.7.1) T_e\sim 6 \ 10^4 K$. Il confronto con la luminosità del Sole $(\sim 10^{33} erg/sec)$ rivela come in tali oggetti supermassivi il rapporto luminosità/massa risulti dell'ordine di $\sim 10^5$ volte di quello solare.
A causa delle elevatissime densità, anche stelle di neutroni che
eventualmente si producano nell'esplosione di Supernovae sono
caratterizzate da campi gravitazionali estremamente intensi, e
necessitano quindi di un trattamento relativistico. Se si assume
che i neutroni si comportino come un gas di fermioni liberi
($\rightarrow A3.2$) per essi vale un equazione di stato del tipo
$$ P = P(\rho)\sim 4 * 10^{19} \rho^{5/3}$$
che, unita alle due precedenti relazioni, consente di definire la
struttura dell'oggetto (caso politropico $\rightarrow
A5.1$). Se ne ottiene una relazione massa-densità centrale che
raggiunge un massimo per $M=0.7M_\odot$ (Fig.2.8). E' subito visto
che strutture al di sopra di tale limite non sono stabili: una
fluttuazione della densità centrale porterebbe la stella fuori
dall'equilibrio, innescando una contrazione e,di qui, un processo
di collasso reazionato positivamente.
L'approssimazione di un gas di fermioni appare peraltro inadeguata, perchè a densità che raggiungono e superano quelle nucleari interverranno certamente interazioni a molti corpi tra le particelle. Equazioni di stato più realistiche appaiono spostare il precedente limite sino a 2-3 $M_\odot$ (Fig. 2.8). Al di sopra di queste masse non si trovano meccanismi in grado di fermare il collasso della struttura, che dovrebbe quindi procedere indefinitamente.
Al riguardo è facile verificare come l'equazione dell'equilibrio
presenti una singolarità per
$$r=\frac{2GM}{c^2}$$
E' questo il cosiddetto raggio di Schwarzschild. Anche
nell'approssimazione non relativistica si verifica facilmente che,
per ogni massa, a tale raggio corrisponde una velocità di fuga
pari alla velocità della luce. In generale si trova che quando il
collasso raggiunge il raggio di Schwarzschild i fotoni non sono
ulteriormente in grado di sfuggire dall'oggetto collassante, che
quindi cessa di avere un tale canale di comunicazione
elettromagnetica con il resto dell'Universo (diventando una
buca nera).
