A3.2 Degenerazione elettronica. Equazione di stato di un gas di Fermi
La teoria cinetica dei gas, così come sviluppata nella meccanica statistica, mostra come il concetto di temperatura sia indissolubilmente connesso col concetto di equilibrio termico.Il principio fondamentale è che per ogni prefissato insieme di N particelle contenute in un volume V e di assegnata energia totale E tutte le possibili configurazioni microscopiche compatibili con le assegnate condizioni sono equiprobabili. Ne segue che il macrostato che finisce con il realizzarsi è quello cui corrisponde la massima probabilità, cioè il maggior numero di microstati. E' questo quello che noi chiamiamo equilibrio termico. L'obiettivo primario della meccanica statistica è dunque quello di valutare tutti i diversi possibili stati microscopici corrispondenti ad una assegnata energia totale E delle particelle del sistema. E' noto come su questa base si giunga alla nota distribuzione di Maxwell-Boltzmann per la velocità delle particelle a prefissata temperatura T.
La considerazione della natura quantistica delle particelle
introduce, salvando il principio, notevoli modifiche al calcolo
classico delle configurazioni microscopiche. Dal
principio di
indeterminazione di Heisenberg (secondo il quale $\Delta p_x \Delta x= h$) si
ricava che il numero di stati permessi per una particella
contenuta in un volume V e con quantità di moto p compresa tra
p e p+dp è dato da
$$ \Delta N= \frac {1}{h^3} 4\pi p^2 dp V = g(p)dp V$$
dove g(p) rappresenta la densità degli stati. La
distribuzione delle particelle in tali possibili stati deve essere
valutata con l'ulteriore avvertenza che la meccanica quantistica
opera su particelle indistinguibili, il che implica che non
si devono considerare distinti due stati se due particelle si sono
solo scambiate di posto. Tale distribuzione dipende infine da
proprietà globali delle particelle che, in natura, appartengono
ad una delle due classi:
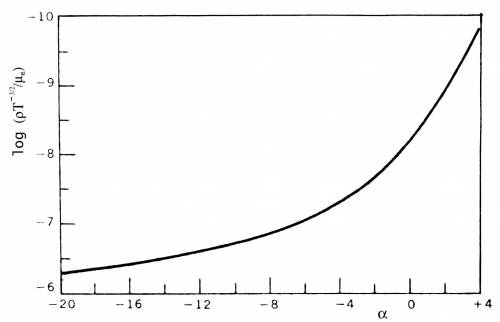
Figura 3.12 Il valore del parametro $\alpha$ al variare
di $\rho T^{-3/2}/ \mu_e$
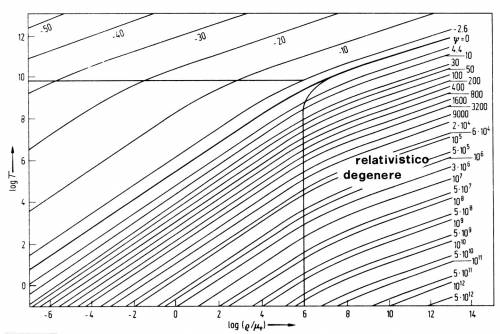
Figura 3.13 Mappatura nel piano $\rho / \mu_e$, T del
valore del parametro di degenerazione $\Phi$ = -$\alpha$
Per le particelle a spin semiintero sussiste l'ulteriore
condizione (principio di esclusione di Pauli) secondo la
quale uno stato non può essere occupato da più di una
particella, da cui discende che non più di due elettroni (con
spin opposto) possono occupare uno stato di moto, talchè
$g(P)=8\pi p^2/h^3$. Se ne trae la
statistica di Fermi-Dirac,
secondo la quale, detta $n(p)dp$ la densità di
elettroni tra p e p+dp,
$$n(p)dp = \frac{2}{h^3}4\pi p^2 dp P(E)$$
dove l'indice di occupazione $P(E)$ di uno stato è dato da
$$P(E)=1/(e^{\alpha +E/kT}+1)$$
e dove, per ogni assunto valore della densità di elettroni $n_e$
e e della temperatura T, il valore di $\alpha$ resta determinato
della condizione
$$\int n(p)dp=n_e $$
Poichè $\rho= n_e \mu_e H$, il valore di $\alpha$ resta fissato
per ogni coppia di valori $T, \rho/\mu_e$ (Figg. 3.12, 3.13)
Si noti come in ogni caso $P(E)\leq 1$ come
vuole il principio di esclusione di Pauli. Al crescere di $n_e$
decresce $\alpha$, che da valori grandi e positivi (gas classico)
raggiunge grandi valori negativi (gas degenere). Nel caso di gas
classico P(E)« 1 per tutte le energie. Nel caso completamente
degenere $\alpha << 0$ e
P(E)=1 per $$E/kT<|\alpha|$$
P(E)=0 per $$E/kT>|\alpha|$$
cioè tutti gli stati sono occupati sino all'energia
$$ E = |\alpha kT|$$, che prende il nome di energia di Fermi. In tale caso
$$n_e=\int n(p)dp = \frac {8\pi}{3h^3}p_{max}^3$$
che mostra come al crescere di ne cresce l'energia massima
raggiunta dagli elettroni. Tale accadimento è subito compreso
osservando che in degenerazione completa tutti gli stati ad
energia minore sono occupati, e ove si spingano altri elettroni
nell'unità di volume essi devono andare ad occupare stati ad
alta energia. Si comprende anche come al crescere di ne si
giunga infine a spingere gli elettroni ad energie relativistiche
anche a basse temperature.
Nel caso generale, ed in approssimazione non relativistica, si ha
$E=p^2/2m_e$ da cui
$$n_e=\int n(p)dp = \frac
{8\pi}{h^3}\int_{0}^{\infty}\frac {p^2 dp} {e^{\alpha +
p^2/2m_ekT}+1}$$
con la sostituzione $x=p^2/2m_ekT$ si ottiene
$$n_e= \frac
{4\pi}{h^3} (2m_ekT)^{3/2} \int_{0}^{\infty}\frac {x^{1/2}dx}
{e^{\alpha + x}+ 1}= \frac {8\pi(2m_ekT)^{3/2}}{h^3}
F_{1/2}(\alpha)$$
dove $F_{1/2}(\alpha)$, come definito dalle precedenti relazioni,
prende il nome di funzione “1/2” di Fermi. Come già
ricavato per il caso del gas perfetto ($\rightarrow A2.1$), la
pressione elettronica discende dal momento trasportato, da cui
$$P_e=\frac {1}{3}\int_{0}^{\infty}pv_e n(p)dp= \frac
{8\pi(2m_ekT)^{3/2}}{3h^3}kT F_{3/2}(\alpha)$$
con analoga definizione della funzione di Fermi $F_{3/2}$. Per la
pressione del gas si può quindi porre
$$P=P_i+P_e=\frac {k}{\mu H}\rho T+ \frac {8\pi(2m_ekT)^{3/2}}{3h^3}kT F_{3/2}(\alpha)$$
Ricordando che $n_e=\rho/\mu_e H$ si ottiene infine
$$P=P_i+P_e=\frac {k}{\mu H}\rho T [1+\frac {\mu}{\mu_e}\Phi (\alpha)]$$
dove $$\Phi(\alpha)=2/3(F_{3/2}/F_{1/2})$$
rappresenta il contributo addizionale portato alla pressione dalla
degenerazione elettronica.
Per ogni coppia di valori
$$\rho,T$$ è possibile ricavare il valore di $$\alpha$$ e per ogni
$$\alpha$$ ottenere P dalle correnti tabulazioni di $F_{1/2}$ e
$F_{3/2}$ (Fig. 3.14).
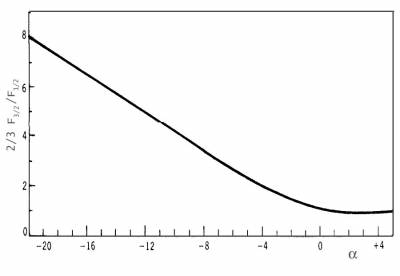
Figura 3.14 Il rapporto 2/3 F$_{3/2}$/F$_{3/2}$, che
rappresenta la correzione di degenerazione alla pressione di gas
perfetto, in funzione del parametro $\alpha$.
In letteratura è frequentemente utilizzato il parametro di
degenerazione $\Psi= -\alpha$. Si può mostrare che $\Psi kT$
fornisce il potenziale termodinamico di Gibbs per elettrone. Per
$$\Psi < -4$$ il gas di elettroni ha un comportamento classico,
$$-4 < \Psi < 4 $$ rappresenta la zona di degenerazione parziale, mentre
per $$\Psi > 4$$ nel gas domina la pressione di degenerazione.
Notiamo infine che la presenza di degenerazione elettronica
modifica anche il comportamento termodinamico che abbiamo studiato
nel caso di una miscela di gas perfetto e radiazione
($\rightarrow A2.1$). Utilizzando la stessa linea di ragionamento adottata in
quella occasione, dovremo portare
$$Tds=dU-\frac {P}{\rho^2}d\rho$$
nella forma
$$TdS=C_P dT - E_P dP$$
ricordando però che ora
$$\rho=\rho(\Psi,T)$$
$$P=P_e(\Psi,T)+P_i(\rho,T)+P_r(T) = P(\Psi,T)$$
Con una lunga serie di passaggi e sostituzioniè possibile
ottenere $d\Psi$ in funzione di P, T, $\rho$, $\Psi$, dP, dT, e
utilizzando la formula di ricorrenza per le funzioni di Fermi
$$\frac {dF_n(\Psi)}{d\Psi}= nF_{n-1}(\Psi)$$
si ottiene infine
$$C_P=\frac {P}{\rho T}(\frac {HP}{\rho kT}\frac{(4-3\beta /2)^2}{L(\Psi)}-\frac {15}{4}\beta)$$
$$E_P=\frac {1}{\rho}(\frac {HP}{\rho kT}\frac{(4-3\beta /2)}{L(\Psi)}-\frac {3}{2})$$
dove
$$L(\Psi)=\frac {1}{\mu_i}+\frac {2}{\mu_e}\frac {F_{1/2}(\Psi)}{F_{-1/2}(\Psi}$$
e $\beta = P_G/P = (P_i+P_e)/P$ essendo P, come di consueto,
la pressione totale. Al limite di non degenerazione
($\Psi \rightarrow -\infty$) $L(\Psi)$ tende a $1/\mu_i + 1/\mu_e$
e le relazioni
precedenti si riconducono alle corrispondenti formule per un gas non degenere.
Nel caso di completa degenerazione è facile ricavare
direttamente le relazioni tra pressione e densità. Nel caso non
relativistico per la quantità di moto si ha $p=m_e v_e$, da cui
$$P_e =\int_{0}^{p_{max}} p v_e n(p) dp =\int_{0}^{p_{max}} \frac {p^2}{m_e} \frac {8 \pi p^2}{h^3}dp = \frac {8 \pi}{15} \frac {p_{max}^5}{m_e h^3}$$
e poiché
$$n_e = \frac {8 \pi}{3} \frac {p_max^3}{h^3}$$
ricordando che $n_e = \rho /\mu_e H$ si ricava infine
$$P_e =(\frac {3}{8 \pi})^{2/3}\frac {h^2}{5 m_e H^{5/3}} (\frac
{\rho}{\mu_e})^{5/3}$$.
Nel caso relativistico
$$p= \frac{m_e v_e}{(1-v_e^2/c^2)^{1/2}} \ {\rm da \ cui} \ v_e = \frac {pc}{[(m_e c)^2 + p^2]^{1/2}}$$
dalla quale, con percorso analogo al caso precedente non
relativistico
$$P_e = \frac {1}{8} (\frac {3}{\pi})^{1/3} \frac {hc}{H^{4/3}} (\frac {\rho}{\mu_e})^{4/3}$$
