5.3. La presequenza
Alcune semplici considerazioni permettono di predire come debba
presentarsi una struttura stellare nelle prime fasi che seguono la
sua formazione. Essa sarà ovviamente espansa, essendo giusto
all'inizio della sua lunga storia di contrazione, ma anche
relativamente fredda, perchè la stabilizzazione della struttura
segue, come abbiamo già ricordato, l'inizio della ionizzazione
parziale dell'idrogeno. Poichè dalla relazione di corpo nero
segue che grandi raggi implicano anche grandi luminosità, si
giunge alla conclusione che al momento della sua formazione una
struttura deve presentarsi relativamente fredda ma molto luminosa:
in termini astronomici deve presentarsi come una Gigante Rossa.
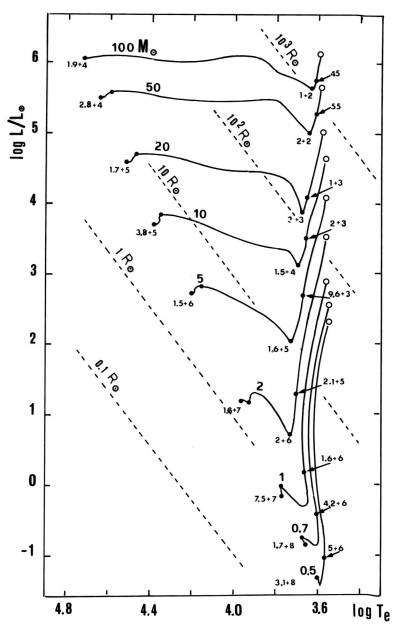
Fig. 5.1 Tracce teoriche per l'evoluzione
presequenza di stelle di varie masse e composizione chimica
solare. Nel diagramma sono anche indicate le linee di raggio
costante come ricavabili dalla relazione di corpo nero
L=4$\pi$R$^2 \sigma$ T$_e^4$. I cerchietti aperti indicano le fasi
iniziali di contrazione gravitazionale. Il primo punto sulla
traccia segnala l'ultimo modello totalmente convettivo, il
penultimo punto il primo modello sorretto nuclearmente e l'ultimo
il modello di Sequenza Principale di Età Zero. I tempi lungo le
tracce sono in anni.
Tale previsione è puntualmente verificata dai risultati del
calcolo. La Fig. 5.1 mostra la posizione nel diagramma
HR teorico (logL, logTe) di modelli stellari con composizione
chimica solare nelle primissime fasi di contrazione
gravitazionale. Come atteso, tutti i modelli sono completamente
convettivi, e tali rimangono per il primo tratto di evoluzione che
si svolge con una decrescita della luminosità a temperatura
pressochè costante, e quindi con una sensibile diminuzione del
raggio. All'aumentare della temperatura centrale diminuisce
l'opacità e al punto indicato in figura incominciano a formarsi
dei nuclei in equilibrio radiativo. Al crescere di tale nucleo la
traccia evolutiva abbandona infine il precedente andamento per
spostarsi verso alte temperature con un contenuto aumento di
luminosità. Mostreremo nel seguito come sia proprio la presenza
di un nucleo radiativo a spostare la stella verso alte temperature
efficaci, abbandonando quella che viene indicata in letteratura
come la “Traccia di Hayashi”.
Mentre la stella si sposta verso alte temperature cominciano a diventare efficienti le reazioni nucleari sinchè (penultimo punto in Fig. 5.1) l'energia nucleare arriva a coprire l'intero fabbisogno energetico della struttura, svanisce il contributo dell'energia gravitazionale e ha termine la fase di contrazione su tempi scala termodinamici. In linea del tutto generale è da notare come tutte le stelle si stabilizzino attorno a quella che sarà la loro luminosità nella fase di combustione nucleare ben prima che le reazioni stesse comincino a diventare efficienti, a ulteriore riprova che non sono le reazioni a determinare la luminosità di un oggetto stellare. E' vero il contrario: la luminosità, governata dalle condizioni di equilibrio, determina la richiesta di energia e quindi l'efficienza delle reazioni nucleari.
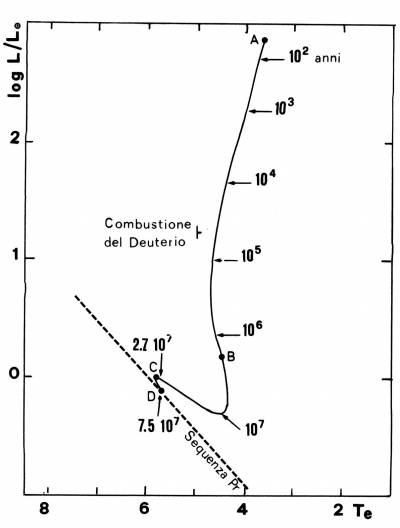
Fig 5.2
Evoluzione di presequenza per una stella di
1 M$_{\odot}$ e composizione chimica solare. A= modello iniziale;
B= ultimo modello completamente convettivo; C= primo modello
sorretto nuclearmente; D= Sequenza principale di Età Zero
(ZAMS). Lungo la traccia sono riportati i tempi di evoluzione ed
i modelli in cui si raggiungono le temperature centrali per la
combustione del deuterio.
La Fig. 5.2 riporta con qualche ulteriore dettaglio
la traccia di presequenza per una stella di 1 M$_{\odot}$.
L'evidenza che l'evoluzione rallenti al diminuire della
luminosità non dovrebbe sorprendere: la luminosità altro non
è che l'energia persa dalla struttura per unità di tempo, e in
fase di contrazione gravitazionale l'evoluzione sarà tanto
più veloce quanto più veloce la perdita di energia. Nella
stessa figura sono indicati i modelli in cui per la prima volta si
raggiungono le temperature per la combustione del deuterio. La
scarsa abbondanza naturale di questo elemento rende pressochè
trascurabile il contributo di tali combustioni, causando al più
un transitorio rallentamento dell'evoluzione.
In base a semplici considerazioni sui tempi scala nucleari noi abbiamo già identificato la Sequenza Principale osservata, ad esempio, nelle stelle nei dintorni del Sole, come formata da strutture in fase di combustione di idrogeno. Possiamo perfezionare tale identificazione precisando che definiremo stelle di Sequenza Principale tutte quelle stelle che evolvono con i tempi scala della combustione dell'idrogeno. Sulla base di tale definizione si deve concludere che il primo modello sorretto nuclearmente al termine della fase di contrazione NON rappresenta ancora una struttura di Sequenza Principale. Nei meccanismi di combustione dell'idrogeno, siano essi la catena pp o il ciclo CNO, vi sono infatti specie nucleari che devono portarsi all'equilibrio prima che la combustione dell'idrogeno raggiunga una situazione di regime e che evolveranno - e con essi la struttura - con tempi scala intermedi tra quelli gravitazionale e quelli della combustione dell'idrogeno. Conseguentemente dovremo definire come primo modello di Sequenza Principale (o modello di ZAMS = Zero Age Main Sequence) il primo modello sorretto nuclearmente in cui gli elementi secondari abbiano raggiunto l'equilibrio.
Nel caso di una stella di 1 M$_{\odot}$, quale quello illustrato
in Fig. 5.2, la struttura arriva ad essere sorretta
dalle combustioni nucleari con temperature centrali dell'ordine
dei 15 106 K, alle quali domina ancora la catena PPI. Per
arrivare al modello di ZAMS dovremo quindi attendere che l'
$^3$He, pressoché ancora nullo nel primo modello sorretto
nuclearmente, raggiunga la sua composizione di equilibrio. E'
istruttivo riconoscere in Fig. 5.3 il comportamento
della struttura in questa fase di approccio alla sequenza
principale. Durante tutta la fase di contrazione gravitazionale
temperatura e densità centrale aumentano con continuità sino a
quando intervengono le reazioni nucleari e l'energia prodotta
dalla gravitazione crolla rapidamente a zero, sostituita da
quella nucleare.
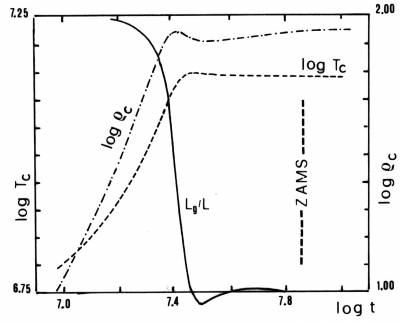
Fig. 5.3
Andamento col tempo di temperatura
centrale, densità centrale e energia gravitazionale in una
stella di 1 M$_{\odot}$ durante la fase di contrazione e
nell'approccio alla Sequenza Principale.
Per mancanza d $^3$He le reazione $^3$He+$^3$He $\rightarrow$
$^4$He + 2p non può essere efficiente, e la combustione si deve
limitare alla produzione di $^3$He, con l'emissione di energia
corrispondente alla sola produzione di tale elemento,. Mano a mano
che aumenta l'abbondanza di $^3$He, la $^3$He+$^3$He $\rightarrow$
$^4$He + 2p comincia a diventare efficiente, il PPI si completa e
aumenta l'energia prodotta per ogni fusione di coppia di protoni,
aggiungendovisi l'energia guadagnata nella produzione dell'$^4$He.
La stella, che si era portata a temperature tali da soddisfare al
suo fabbisogno energetico con il solo PPI incompleto, reagisce
all'eccesso di energia diminuendo temperatura e densità per
abbassare la velocità delle reazioni e mantenere costante la
produzione di energia nucleare. Ne segue anche una espansione con
il limitato assorbimento di energia gravitazionale segnalato dai
valori negativi in figura. E' temporaneamente presente un piccolo
nucleo convettivo, destinato ad una rapida sparizione e privo di
conseguenze evolutive ($\rightarrow$ A5.4).
La decrescita della temperatura prosegue sinchè l'$^3$He nelle
zone di combustione si stabilizza alla sua composizione di
equilibrio: da questo momento la stella cessa di evolvere con i
tempi scala dell'equilibrio dell'$^3$He e inizia ad evolvere con i
tempi scala della combustione dell'idrogeno (modello di ZAMS).
Durante la fase di riaggiustamento nucleare che intercorre tra il
primo modello sorretto nuclearmente e il modello di ZAMS le
condizioni centrali tornano verso valori precedenti e,
corrispondentemente, come mostrato nelle figure 5.1 e
5.2 si inverte la direzione della traccia nel
diagramma HR.
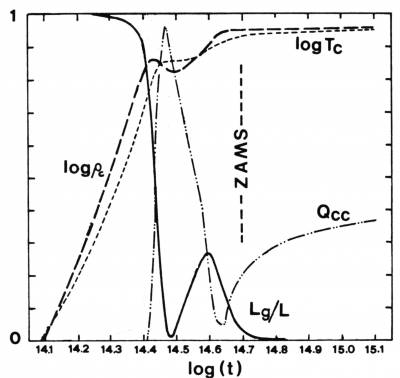
Fig. 5.4
Andamento col tempo di temperatura
centrale, densità centrale e energia gravitazionale in una
stella di 1.5 M$_{\odot}$ durante la fase di contrazione e
nell'approccio alla Sequenza Principale. Q$_{cc}$ riporta
l'estensione del nucleo convettivo in frazioni di massa stellare.
Estremi delle ordinate: 0.80 $\le$ logT$_c$ $\le$ 1.39; 0.75 $\le$
log$\rho_c$ $\le$ 2.00
Al diminuire della massa il diminuire della temperatura centrale dei
modelli sorretti nuclearmente causa la drastica diminuzione della
luminosità intrinseca delle strutture. Le reazioni nucleari
continuano dunque ad essere dominate dalla catena PPI e le fasi di
presequenza hanno andamenti sostanzialmente analoghi, almeno
sinchè non si giunga (M $\le$ 0.4 M$_{\odot}$) a temperature
centrali così basse e, conseguentemente, a tempi di equilibrio
dell'$^3$He così grandi da configurare per tale elemento il
ruolo di elemento primario. In tal caso svanisce la fase di
rilassamento nucleare e il primo modello sorretto nuclearmente
deve essere considerato modello di ZAMS.
Ancora analogo, ma per alcuni versi speculare, l'avvicinamento alla Sequenza Principale di modelli invece più massicci, nei quali la maggior richiesta di energia conduce a maggiori temperature centrali, portando alla dominanza del ciclo CNO. L'equilibrio del ciclo viene raggiunto quando il $^{12}$C viene trasformato in $^{14}$N, diminuendo la velocità del ciclo e l'energia emessa nell'unità di tempo. La Fig. 5.4 mostra che in tal caso al primo modello sorretto nuclearmente segue un nuovo episodio di limitata contrazione e un ulteriore aumento di temperatura che infine consente al ciclo all'equilibrio di fornire la richiesta energia. Nel diagramma HR il modello prosegue ora la sua traccia, innalzando ulteriormente la temperatura efficace. Notiamo infine che, come previsto ($\rightarrow$ Cap. 2), a causa della alta dipendenza dalla temperatura la combustione CNO produce ora nuclei convettivi, che si manterranno per tutta la fase di sequenza principale.
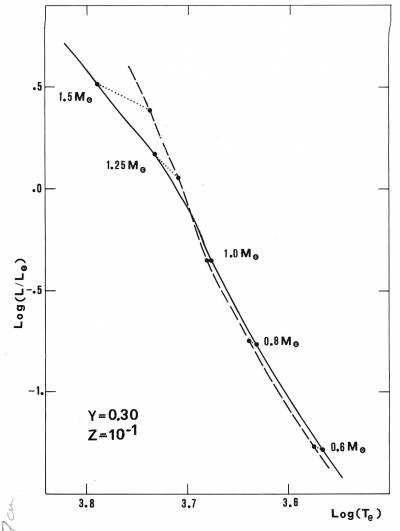
Fig. 5.5 Una sequenza di modelli omogenei
supermetallici (linea a tratti) confrontata con la collocazione
dei modelli di ZAMS.
La diversa risposta delle combustioni pp e CNO nell'approccio
all'equilibrio si riflette quindi nella diversa collocazione nel
diagramma HR dei modelli di ZAMS rispetto ai modelli omogenei
sorretti nuclearmente. Come mostrato in Fig. 5.5
modelli di ZAMS sorretti dalla catena pp si collocano a
temperature efficaci leggermente inferiori dei rispettivi modelli
omogenei, mentre il contrario avviene per i modelli sorretti dal
CNO, che continuano la contrazione per portarsi a temperature
efficaci più alte. Tale diversa risposta rende anche ragione del
fatto che alla transizione tra le due combustioni esiste un
intervallo di masse in cui i modelli omogeni sono sorretti dal CNO
e i modelli di ZAMS dal pp. La massa di transizione dipende
naturalmente dalla assunta composizione chimica: innalzando l'elio
originario si ottengono, ad esempio, modelli più caldi e la
massa di transizione diminuisce.
Resta infine da osservare come, sulla base delle considerazioni svolte, si possa concludere che la struttura di un modello di ZAMS possa in genere essere identificata anche senza procedere al calcolo dettagliato delle fasi di presequenza. Sinchè, come avviene per masse non troppo piccole, i tempi scala gravitazionale, nucleare dei secondari e nucleare del'idrogeno restano ben distinti, sarà lecito integrare direttamente un primo modello omogeneo sorretto nuclearmente imponendo $\varepsilon$=0, e lasciando evolvere la struttura sino a raggiungere l'equilibrio dei secondari (pseudoevoluzione).
