5.4. La traccia di Hayashi
Si è visto come tutti i modelli stellari nella loro iniziale fase convettiva seguano ben definite e tra loro analoghe sequenze confinate alle basse temperature efficaci. Tale comportamento va inquadrato in una regola generale secondo la quale per ogni prefissata massa e composizione chimica esiste nel diagramma HR un limite destro invalicabile definito appunto da strutture totalmente convettive, che prende il nome di traccia di Hayashi. Tale regola, enunciata nel 1961 dall'astrofisico giapponese Kushiro Hayashi sulla base di modelli stellari semianalitici, può essere convenientemente illustrata in base ad esperimenti numerici.
Si riprendano infatti le equazioni di equilibrio e si consideri il
gradiente dT/dp come un parametro libero G costante lungo la
struttura. Se ne ricava il sistema politropico
$dP/dr = \ldots.$
$dM_r/dr = \ldots$
$dT/dp = G$
che per ogni valore di G e per ogni assunto valore della
luminosità L ammette una soluzione. Non sorprendentemente, si
trova che per ogni L, al crescere di G il modello (non realistico)
si sposta a temperature efficaci minori. Il criterio di
Schwarzschild detta peraltro un limite superiore per i valori del
“gradiente medio” G, dovendo risultare
$$\frac {dT}{dP} \le (\frac{dT}{dP})_{ad}$$
ove, trascurando gli effetti superficiali di superadiabaticità,
l'eguaglianza implica strutture completamente convettive. Ne segue
che la linea formata al variare di L da tali strutture convettive
rappresenta nel diagramma HR un limite destro per strutture in
quasi equilibrio.
E' utile inserire il concetto di traccia di Hayashi nel contesto
più vasto di un indagine topologica della convezione negli
strati esterni delle strutture stellari. Si è già indicato
come al diminuire della temperatura efficace ci si attenda che
nascano e progressivamente si sviluppino in profondità strati
convettivi superficiali collegati alla ionizzazione parziale
dell'idrogeno. Tale previsione qualitativa può essere
perfezionata osservando che il metodo del “fitting” ci assicura
che per ogni prefissata massa stellare, ogni posizione del
diagramma HR (ogni coppia di valori L e Te) identifica senza
ambiguità le condizioni superficiali. E' lecito quindi integrare
le equazioni di equilibrio verso l'interno, identificando le
catatteristiche che avrebbe la struttura e, in particolare, la
profondità degli strati convettivi, se presenti. Si noti che in
tale modo non si esegue la valutazione di un reale modello
stellare: si opera solamente la previsione che se una stella di
data massa si venisse a trovare in quel punto del diagramma HR,
allora dovrebbe avere la struttura esterna così calcolata.
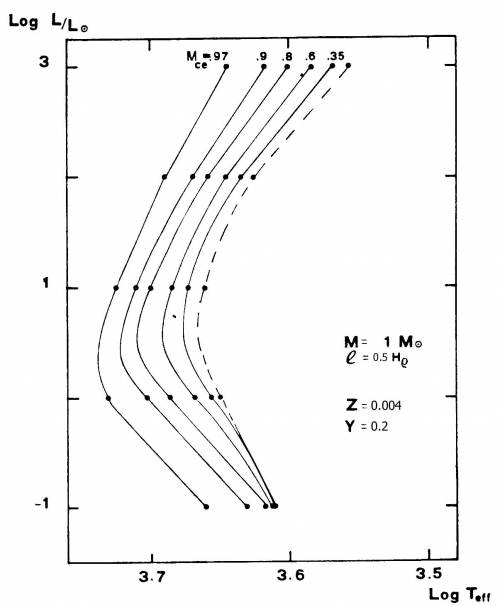
Fig. 5.6 Linee isoconvettive HR per una struttura di
1 M$_{\odot}$ dalla indicata composizione chimica. Le singole
linee indicano il luogo nel diagramma HR ove la base
dell'inviluppo convettivo raggiunge un prefissato valore della
frazione di massa Mce. La linea a tratti riporta la traccia di
Hayashi (strutture totalmente convettive).
Tali informazioni possono essere accorpate per produrre la
topologia degli inviluppi convettivi mostrata in
Fig. 5.6, ove le varie linee isoconvettive
rappresentano il luogo dei punti ove la convezione superficiale
affonda sino ad un predeterminato valore della massa stellare.
Come caso limite, si ottiene così anche una valutazione della
traccia di Hayashi ove sono tenuti in debito conto gli effetti
della superadiabaticità.
Poichè i modelli di presequenza percorrono per definizione le
rispettive tracce di Hayashi, la precedente Fig. 5.1
mostra chiaramente come al diminuire della massa stellare la
traccia di Hayashi si sposti verso temperature efficaci minori. La
Fig. 5.7 mostra come la traccia si sposti verso minori
temperature efficaci anche all'aumentare della metallicità. La
sensibilità al contenuto originario di elio è molto minore,
almeno nel campo delle variazioni attese per questo parametro
evolutivo ($\Delta$ Y $\le$ 0.1), con la traccia che si sposta
leggermente a temperature inferiori al diminuire di Y. La
particolare sensibilità al contenuto metallico discende dal
forte contributo dato dai metalli (a differenza dell'elio)
all'opacità della materia.
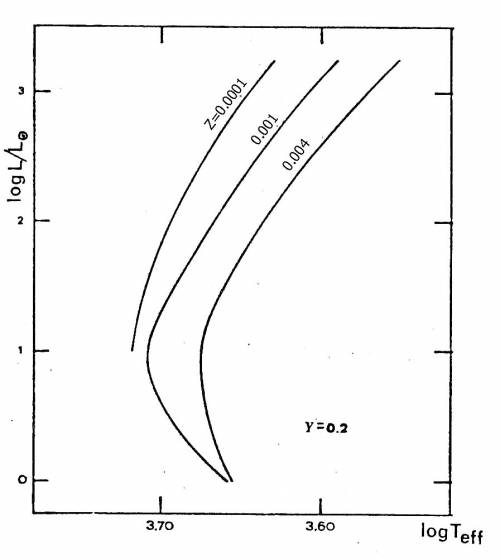
Fig. 5.7 Tracce di Hayashi per una struttura di
1 M$_{\odot}$ al variare del contenuto metallico.
E' infine di particolare rilevanza osservare che per ogni fissata
massa e composizione chimica originaria la traccia di Hayashi
dipende anche, e sensibilmente, dalla lunghezza di rimescolamento
adottata nel trattamento della convezione superadiabatica. Minore
la lunghezza di rimescolamento, meno efficiente è il trasporto
convettivo e più alto il valore della superadibaticità. Si
noti al riguardo come al limite $l \rightarrow$0 debba risultare
anche $\nabla_{con} \rightarrow \nabla_{rad}$. Maggiore
superadiabaticità significa infine maggiori gradienti
all'interno della struttura e di conseguenza temperature più
basse in atmosfera. Se ne conclude che al diminuire di $l$ la
traccia di Hayashi si sposta, come avviene, verso temperature
più basse. Se ne deve concludere che in assenza di indicazioni
precise sul valore di $l$ ($\rightarrow$ A5) la collocazione
della traccia è soggetta a pesanti incertezze, che si riflettono
non solo sulla temperatura delle tracce di presequenza, ma anche,
come vedremo, sulla collocazione nel diagramma HR delle Giganti
Rosse.
