A7.3 Rotazione stellare. ZAHB rotazionali
Non sorprendentemente, l'evidenza sperimentale mostra che non solo
il Sole ma anche le altre stelle ruotano attorno ad un loro asse.
Evidenze per la rotazione stellare possono essere e sono ricavate
dall'allargamento delle righe di assorbimento dovuto all'effetto
Doppler, qualora l'asse di rotazione della struttura non giaccia
lungo la linea visuale. La Fig. 7.31 riporta
l'andamento della velocità equatoriale media caratterizzante
stelle di SP di varia massa. Si nota come al di sotto di
$\sim$ 2 M$_{\odot}$ si evidenzi una brusca diminuzione dello stato di
rotazione. Ciò viene posto in relazione con l'instaurarsi di una
zona di convezione superficiale e, con essa, di un vento solare in
grado di estrarre momento angolare dalla struttura, tramite
l'interazione delle particelle del vento col campo magnetico
ruotante originato dalla struttura medesima. A parziale riprova di
questa interpretazione vi è l'osservata correlazione inversa tra
l'età della struttura e le velocità di rotazione.
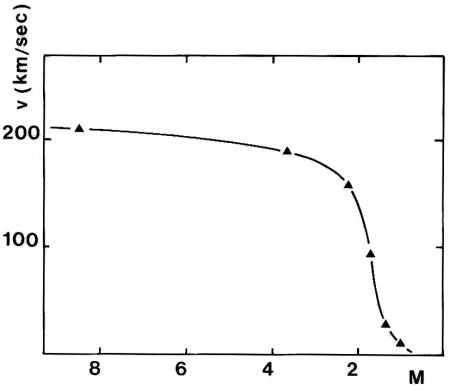
Fig. 7.31 Andamento con la massa stellare delle
velocità equatoriali medie per stelle di Sequenza Principale. Le masse sono in
masse solari.
La rotazione stellare è un possibile parametro evolutivo che
abbiamo sinora omesso nelle valutazioni strutturali, assumendone
esplicitamente la trascurabilità, almeno come caso generale.
Ciò è confortato dall'andamento monoparametrico dei diagrammi
CM, nei quali non si manifestano gli effetti di un parametro
stocastico come ci si attende sia la rotazione stellare.
Valutazioni rigorose di strutture ruotanti sono peraltro
estremamente complesse, non fosse altro perchè, venendo a cadere
la simmetria sferica, sarebbe in linea di principio necessario
sviluppare codici di calcolo in coordinate cilindriche.
Valutazioni approssimate indicano che la rotazione tende a
raffreddare gli interni stellari. Si può comprendere tale
risultato osservando che la forza centrifuga va in parte a
bilanciare la gravità, diminuendo le richieste di temperatura
(energia cinetica).
Raffreddando l'interno delle strutture stellari, la rotazione può influenzare l'evoluzione di piccole masse in fase di Gigante Rossa, ritardando il flash dell'elio. Ne discende che strutture di ZAHB provenienti da stelle ruotanti dovrebbero avere masse dei nuclei di elio e perdite di massa maggiori di quanto atteso nel caso canonico non rotante. L'aumento della perdita di massa, fatti salvi ulteriori fenomeni legati alla rotazione, restando collegato al maggior tempo passato in fase di Gigante Rossa. Al riguardo sono state eseguite stime evolutive, sotto la condizione di conservazione del momento angolare lungo tutta la struttura. Ciò implica un forte aumento di velocità angolare nei nuclei di elio delle Giganti Rosse, stante le esigue dimensioni spaziali cui tali nuclei si riducono.
In accordo con tali stime massa del nucleo di elio e luminosità
al flash seguono approssimativamente le relazioni
$$ M_c(\omega) \sim M_{c,0} + 1.44 \omega^{2.16}$$
$$ log L_f \sim log L_{f,0} + 3.8 10^{-3} \omega^2 $$
dove $M_{c,0}$ e $Log L_{f,0}$ rappresentano i valori canonici di
modelli non rotanti e $\omega$ è la velocità angolare dei
modelli di Sequenza Principale, data in rotazioni per giorno. E' da notare che per
$\omega \le$ 5 l'evoluzione dalla Sequenza Principale alle Giganti Rosse
resterebbe sostanzialmente inalterata, gli effetti di rotazione
rivelandosi solo nella fase di combustione di elio.
Dalle discusse proprietà topologiche dei modelli a doppia
sorgente di energia si ricava che l'aumento di Mc e quello
della perdita di massa agiscono entrambi nel senso di spostare un
modello dalla sua posizione canonica verso maggiori temperature
effettive, con modalità che dipendono dallo stato di rotazione
delle singole stelle e dalla relativa efficienza dei due
meccanismi citati. La situazione è illustrata dall'approccio
topologico di Fig. 7.32. Se modeste variazioni sulla
velocità angolare $\omega$, tali cioè da non influenzare il
valore canonico di Mc, producono sensibili variazioni sulla
perdita di massa, l'attesa distribuzione sul ramo orizzontale non
si discosta da una ZAHB canonica, indicata in figura come
$\eta$-ZAHB a sottolineare che la distribuzione è originata
esclusivamente da variazioni di efficienza nella perdita di massa.

Fig. 7.32 La collocazione nel diagramma HR di
sequenza di ZAHB sotto diverse assunzioni della relazione tra
perdita di massa e rotazione. La $\eta$-ZAHB rappresenta la ZAHB
canonica con massa variabili e massa del nucleo costante. La
$\omega$-ZAHB è il luogo di strutture con massa costante e
variabile massa del nucleo di He. I cerchietti aperti mostrano la
distribuzione attesa quando perdita di massa e rotazione sono
combinate secondo le prescrizioni fornite nel testo.
Se, all'altro estremo, variazioni di $\omega$ giungono a variare
sensibilmente Mc senza modificare la perdita di massa, le
stelle si distribuiranno lungo una sequenza caratterizzata dalle
condizioni M circa cost ma Mc variabile. Tali sequenze sono
indicate in figura come $\omega$-ZAHB. E' facile verificare che
per ogni assunta relativa efficienza dei due meccanismi le
possibili sequenze di ZAHB rotazionali devono restare comprese nel
cono avente vertice nel modello canonico non ruotante e avente
come limiti la $\eta$-ZAHB e la $\omega$-ZAHB
passanti per quel punto, discostandosi dalla $\eta$-ZAHB
tanto maggiormente quanto
minore è l'influenza della rotazione sulla perdita di massa.
Le attuali valutazioni dell'influenza della rotazione sulle dimensioni in massa del nucleo di elio e sulla perdita di massa paiono indicare un bilanciamento tra questi due effetti, còme mostrato nella stessa Fig. 7.32. Parrebbe potersi obiettare che le stelle di ramo orizzontale sono stelle di piccola massa che abbiamo trovato essere trascurabilmente ruotanti. Da un lato però non abbiamo probanti informazioni sullo stato di rotazione di tali stelle negli ammassi globulari, né sappiamo quanto il meccanismo di frenamento discusso in precedenza agisca in profondità. In effetti ciò che noi misuriamo è lo stato di rotazione dell'atmosfera stellare e nulla sappiamo su una possibile residua rotazione dell'interno. Se una dispersione dei valori della rotazione fosse all'origine della dispersione delle stelle lungo il Ramo Orizzontale verrebbe ad essere modificata la relazione tra luminosità di HB e composizione chimica iniziale così come ricavata dalle $\eta$-ZAHB ed alla base di molte delle correnti elaborazioni teoriche dei dati osservativi.
