Buona parte delle stelle del disco galattico risultano essere gravitazionalmente legate in sistemi binari o multipli.Se le componenti di tali sistemi sono sufficientemente distanti, il legame gravitazionale influenza solo le orbite degli oggetti, e l'evoluzione delle singole strutture non si discosta da quanto valutato per stelle isolate. In sistemi binari stretti possono invece presentarsi peculiari modalità evolutive, che condizionano pesantemente il destiono delle strutture.

Tali peculiarità trovano la loro origine nelle caratteristiche del campo gravitazionale e dalla forza centrifuga di rotazione cui in un sistemi binario $_{1,2}$ sottoposta la materia. Ponendosi in un sistema solidale con il baricentro, se trascuriamo la distorsione delle due strutture dovute alle mutue attrazioni (approssimazione di Roche) il potenziale gravitazionale è semplicemente fornito da

$$\Phi= - (\frac {GM_1}{r_1}+\frac {GM_2}{r_2})$$

dove M$_{1,2}$ e r$_{1,2}$ sono ripettivamente le masse e le distanze di un generico punto materiale dai due oggetti. Poniamoci ora in un sistema corotante, assumendo il piano dell'orbita come piano x,y e assumendo anche come origine il centro della stella 1 e asse x la congiungente i centri delle due stelle. In tale sistema le coordinate (x, y, z) del baricentro risulteranno ($\mu$a, 0, 0), dove “a” e la distanza (separazione) tra le due componenti e

$$\mu = \frac{M_2}{M_1+M_2}$$

e il potenziale nell'approssimazione di Roche si esplicita nella forma

$$ \Phi =-(\frac {GM_1}{(x^2+y^2+z^2)^{1/2}}+\frac {GM_2}{((x-a)^2+y^2+z^2)^{1/2}}) -\frac{1}{2}\omega^2[(x-\mu a)^2 +y^2]$$
dove $\omega=2\pi/P$ e l'ultimo termine rappresenta il potenziale della forza centrifuga.


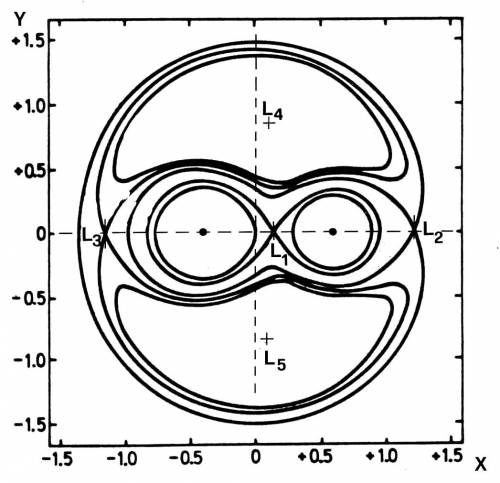
Fig. 11.11 Andamento delle linee equipotenziali nel piano dell'orbita di una binaria. Si è assunto <tex>$\mu$=0.4</tex>

La Fig. 11.11 mostra il complesso andamento delle linee equipotenziali $\Phi=cost$ nel piano dell'orbita nel caso $\mu$=0.4. In prossimità delle stelle predomina il campo dei singoli oggetti mentre, al crecere della distanza, si vanno intrecciando i contributi della gravitazione e della rotazione. A distanze ancora maggiori prevarrà il contributo della rotazione. I cinque punti marcati in figura come L$_i$ rappresentano i cinque punti lagrangiani di equilibro, soluzioni particolare del problema dei tre corpi. Una particella di massa trascurabile ripetto alle altre due componenti, posta in uno dei punti percorrer\`a orbite circolari mantenendo immutata la sua posizione ripetto alle due componenti principali. I punti L$_4$ e L$_5$, posti ai vertici di un triangolo equilatero con base “a”, sono di equilibrio stabile se M$_2 \ll$ M$_1$. Una tale configurazione è realizzata in natura dal sistema Sole-Give- Asteroidi “Troiani”.

Alla superficie equipotenziale passante per <tex>L$_1$</tex> si da il nome di Lobi di Roche. La Fig. 11.12 mostra l'andamento del potenziale lungo la linea congiungente il centro delle due stelle, illustrando nel contempo il principio fondamentale dei meccanismi di trasferimento di massa che regolano l'evoluzione delle stelle nei sistemi bibnari stretti. Sinchè le dimensioni delle singole stelle restano inferiori a quelle dei rispettivi lobi di Roche . l'evoluzione delle strutture segue il cammino delle strutture isolate. L'evoluzione guida peraltro inevitabilmente le strutture verso la fase di Gigante Rossa, con aumenti notevoli di raggio. Se il sistema èsufficientemente stretto (lobi di Roche di dimensioni ridotte) la componente primaria, la più massiccia, evolvendo per prima finirà col riempire il proprio lobo. Ogni tentativo di aumentare ulteriormente il proprio raggio avrà solo l'effetto di reasferire materia sul proprio compagno, “scortecciando” la struttura originale.


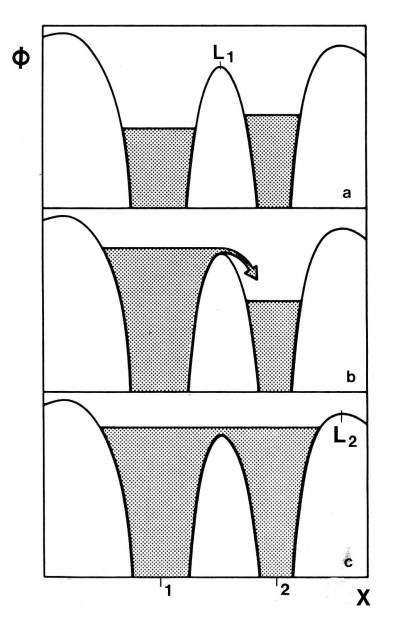
Fig. 11.12 Andamento del potenziale lungo la linea congiungente i centri delle due stelle. La zona ombreggiata indica la regione occupata dalla materia stellare. E' mostrato come al crescere del raggio di una stella si inneschi un meccanismo di trasferimento di massa attraverso il punto lagrangiano <tex>L$_1$</tex>.

E' di grande importanza notare che il trasferimento di massa è fenomeno reazionato positivamente. Ricordando infatti come la traccia di Hayashi si sposti verso il rosso al diminuire della massa, ricaviamo che una gigante, a fissata luminosi\`a, ha raggi tanto maggiori quamto minore è la massa. Per il solo fatto di perdere massa la gigante tende quindi ad espandere ulteriormente il proprio raggio e, come conseguenza, il trasferimento avviene con tempi scala termodinamici anzichè nucleari.

Può così avvenire che l'originale secondaria finisca col diventare la stella più massiccia del sistema, accelerando di conseguenza la sua evoluzione. Al progredire delle fasi evolutive, ogniqualvolta una delle componenti riempi il proprio lobo di Roche si innescheranno fasi di trasferimento di massa. La Fig. 11.12 mostra le tre caratteristiche configurazioni di fatto riscontrate nei sistemi binari

1. Sistemi staccati (detached): le due componenti sono ognuna all'interno del proprio lobo di Roche. Ogni strutura segue una propria caratteristica evoluzione.
2. Sistemi semi-staccati (semi-detached): una delle due componenti riempie il proprio lobo, traferendo materia sull'altra.
3. Sistemi a contatto (common envelope): tutte e due le componenti riempiono contemporaneamente il proprio lobo. La Fig. 11.12 mostra come in simili condizioni il sistema possa perdere massa verso l'esterno attraverso il punto lagrangiano <tex>L$_2$</tex>.

Nei sistemi semi-distaccati o a contatto almeno una delle strutture risulta sensibilmente deformata rispetto alla forma sferica, deformazione che si riflette in precise caratteristiche della curva di luce. A titolo esemplificativo, la Fig. 11.13 mostra la struttura del sistema a contatto AW UMa come derivabile proprio dall'analisi della complessa curca di luce.

Il calcolo dell'evoluzione delle stelle in un sistema binario può essere agevolmente eseguito con solo alcune semplici implementazioni dei normali codici evolutivi per tener conto della presenza dei lobi di Roche, del conseguente fenomeno di travaso delle masse e delle conseguenti variazioni nei parametri orbitali. I risultatisono peraltro molto variegati a fronte dei molti parametri che caratterizzano tali sistemi, quali non solo le masse iniziali delle due componenti ma anche la loro originale separazione. La Fig. 11.14 riporta a titolo di esempio, la storia evolutiva di un sistema con masse iniziali M$_1$ =1.0 e M$_2$ =2.0 M$_{\odot}$. Nella fase “a” ambedue le componenti hanno raggiunto la loro sequenza principale. La primaria M$_1$ evolve per prima sino a riempire il proprio lobo di Roche (fase “b”), iniziando il trasferimento di massa. Nella fase “c” l'originaria secondaria è ormai diventata la componente più massiccia e il sistema è formato da una gigante di 0.8 M$_{\odot}$ che orbita attorno ad una massiccia stella di MS di 2.2 M$_{\odot}$. Nella fase “d” la gigante ha completato la sua evoluzione e il sistema è composto da una Nana Bianca e la massicia stella di MS. L'evoluzione di quest'ultima porta ora al trasferimento di massa sulla Nana, producendo prima esplosioni di Nova (fase “e”) e, infine, una SN di tipoI (fase “f”).


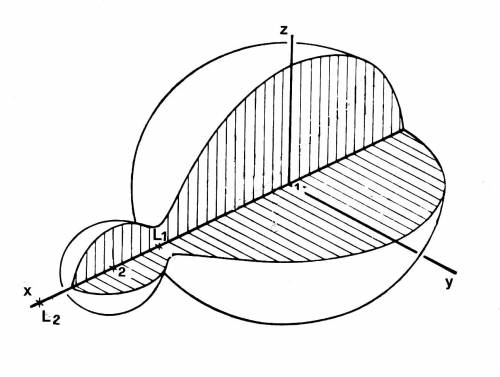
Fig. 11.13 La forma della binaria a contatto AW UMa come ricavata della analisi della curva di luce osservata.

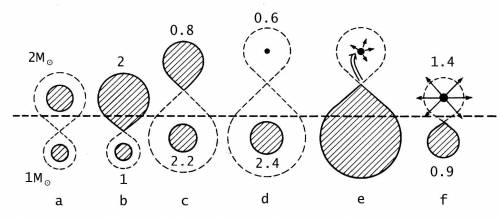
Fig. 11.14 Esempio di evoluzione di un sistema binario di piccole masse.