4.6 Il biciclo CN-NO
Se, e solo se, nel gas stellare è presente anche una minima
quantità di nuclei di carbonio, di azoto e/o di ossigeno, a
temperature leggermente superiori a quelle necessarie per
l'efficienza della catena protone-protone si apre un ulteriore canale di
reazioni per la combustione dell'idrogeno in elio. Se, per
esempio, assumiamo la presenza di soli nuclei di carbonio, a circa
$15 10^6 ∞K$ diventano efficienti processi di cattura protonica
che innescano una serie di reazioni
$^{12}C+p \rightarrow ^{13}N+\gamma$
$^{13}N \rightarrow ^{13}C+e^++\nu \\\ (\tau=870 sec)$
$^{13}C+p \rightarrow ^{14}N+\gamma$
$^{14}N+p \rightarrow ^{15}O+\gamma$
$^{15}O \rightarrow ^{15}N+e^++\nu \\\\ (\tau = 178 sec)$
$^{15}N+p \rightarrow (^{16}O)^* \rightarrow (\sim 99\%)\rightarrow ^{12}C+\alpha$
$^{15}N+p \rightarrow (^{16}O)^* \rightarrow (\sim ~1\%)\rightarrow ^{16}O+\gamma$
Si vede come il nucleo di $^{12}C$ aggreghi successivamente 4
protoni giungendo con l'ultima reazione alla produzione di un
nucleo di $^{16}O$ in uno stato eccitato. Quest'ultimo decade
preferenzialmente restituendo un nucleo di $^{12}C$ ed una
particella $\alpha$ (nucleo di $^4_2He$). Trascurando per il
momento l'ulteriore canale di decadimento in $^{16}O$, siamo
dunque in presenza di un ciclo, in cui il carbonio funge da
catalizzatore della fusione di 4 protoni in un nucleo di elio,
rimanendo disponibile per una serie indeterminata di reazioni.
Naturalmente il ciclo può prendere inizio quando sia presente
almeno uno qualsiasi dei suoi componenti
($^{12}C,^{13}C,^{14}N,^{15}N $), essendosi in precedenza assunto il
$^{12}C$ solo a titolo di esempio. Tale ciclo viene in genere
indicato come ciclo CN ad indicare come esso sia basato
sulla continua mutua trasformazione di questi due elementi.
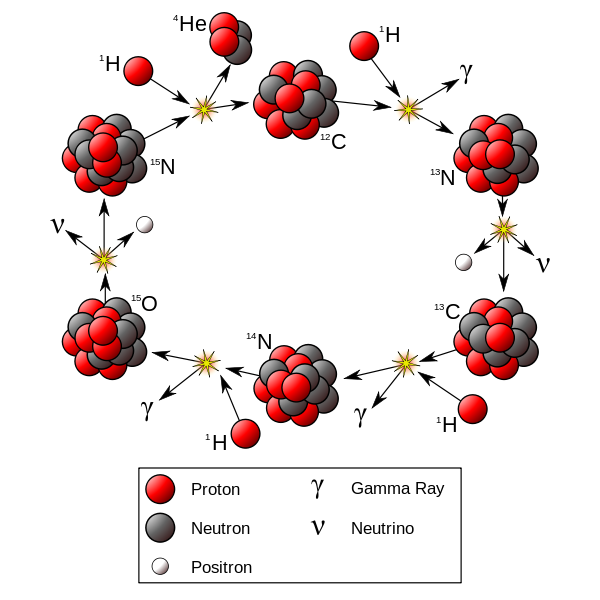 Il biciclo CN-NO (Licenza CC BY-SA 3.0. Attribuzione: Borb)
Il biciclo CN-NO (Licenza CC BY-SA 3.0. Attribuzione: Borb)
Trattandosi di un ciclo, tutti i nuclei C e N sono
contemporaneamente creati e distrutti, e assumono quindi la veste
di elementi secondari, evolventi quindi verso una loro condizione
di equilibrio. All'equilibrio
$n_{1j}=cost$ $(j=12, 13, 14, 15)$ e
per le abbondanze di equilibrio si ricava
$$N(^{12}C)<\sigma_{1,12}v>=N(^{13}C)<\sigma_{1,13}v>=N(^{14}N)<\sigma_{1,14}v>=\ldots.$$
Come atteso, l'abbondanza di equilibrio dei vari nuclei risulta
quindi inversamente proporzionale alla sezione d'urto per i
rispettivi processi di distruzione. La sezione d'urto di gran
lunga minore è quella per processi di cattura protonica su
$^{14}N$, seguita nell'ordine da quelle per gli analoghi processi
su $^{12}C, ^{13}C$ e $^{15}N$. Corrispondentemente ci si attende
che all'equilibrio oltre il 95% dei nuclei sia sotto forma di
$^{14}N$ ed il resto largamente sotto forma di $^{12}C$.
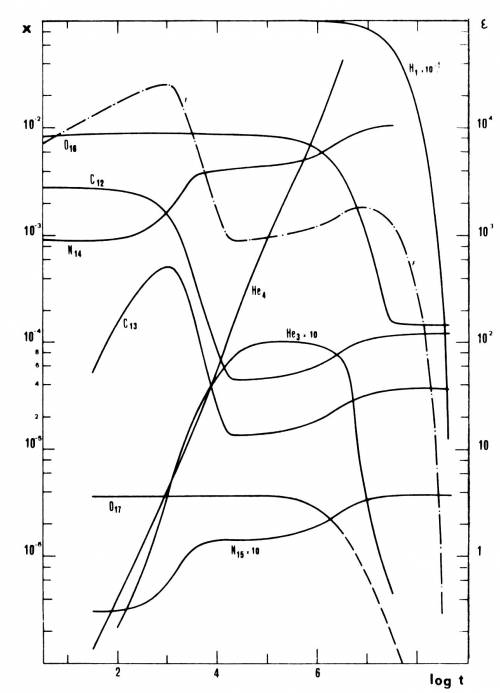
Fig. 4.7 Variazione col tempo dell'abbondanza dei
vari elementi del ciclo CNO in una miscela con composizione
iniziale solare, mantenuta a T= 30*10$^6$ K, $\rho$ = 1
gr/cm$^3$. La linea a tratti mostra l'evoluzione temporale del
coefficiente $\varepsilon$ di generazione di energia. Il tempo t
è in anni
Abbiamo peraltro già indicato come il ciclo CN non sia
perfetto, perdendo una piccola parte dei nuclei a formare
$^{16}O$. Tale perdita è peraltro effimera, perché tale
elemento viene a sua volta processato per restituire nuclei di
$^{14}N$. Si ha infatti
$^{16}O + p \rightarrow ^{17}F + \gamma$
$^{17}F \rightarrow ^{17}O + e^+ +\nu$
$^{17}O + p \rightarrow (^{18}F)^* \rightarrow ^{14}N + \alpha$
ove appare ora lecito trascurare la piccola quantità di
$^{18}F$ che decade nel suo stato fondamentale. Si vede come le
precedenti reazioni realizzino un nuovo ciclo NO: un nucleo di
azoto può aggregare successivamente 4 protoni per restituire
infine ancora un nucleo di azoto più una particella $\alpha$.
Siamo dunque in presenza di due cicli mutuamente accoppiati che
realizzano il cosiddetto biciclo CN-NO nel quale tutti i
nuclei pesanti coinvolti si presentano come elementi secondari. Si
noti che, poichè i nuclei non sono in realtà nè creati
nè distrutti ma solo trasformati l'uno nell'altro, in ogni
caso ed in ogni momento il numero originale N0 di nuclei
pesanti deve conservarsi, risultando
$$\Sigma N_i = N_0$$
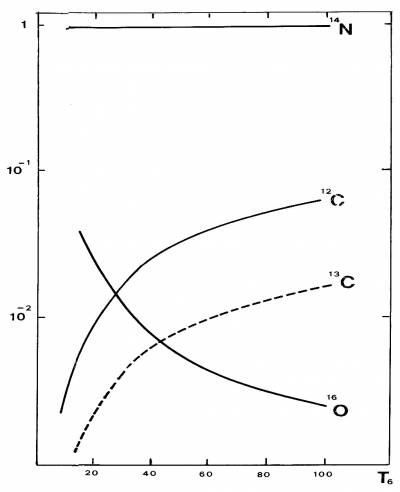
Fig. 4.8 Abbondanze relative di equilibrio al
variare della temperatura (in milioni di gradi) per gli elementi
principali del ciclo CNO. Si è posto $\Sigma N_i = 1$
Alle minori temperature la cattura $^{16}O + p$ è largamente
innefficiente e la combustione riposa essenzialmente sul solo
ciclo CN. Attorno ai $20*10^6 ∞K$ ambo i cicli sono in piena
efficienza e sia $^{12}C$ che $^{16}O$ vengono ridotti a pochi
percento di $^{14}N$. Anche in questo caso la grande maggioranza
dei nuclei di $^{14}N$ finiscono necessariamente con l'evolvere
lungo il ciclo CN che fornisce quindi in ogni caso il maggior
contributo alla generazione di energia. L'importanza del ciclo NO
discende dall'evidenza che il gas interstellare da cui originano
le stelle risulta in genere relativamente ricco di elementi
multipli di $\alpha$, quali $^{12}C$ e $^{16}O$, a fronte di una
relativa sottoabbondanza di $^{14}N$. L'efficienza del ciclo NO ha
dunque l'effetto di rendere disponibili per il ciclo CN gli
originali nuclei di $^{16}O$ presenti nella materia.
Quanto sinora esposto ha come importante conseguenza che l'efficienza
di una combustione CNO viene dunque memorizzata nella abbondanza
relativa di quei tre elementi, secondo lo schema:
Gas non processato $^{12}C$ $\Uparrow$ $^{14}N$ $\Downarrow$ $^{16}O$ $\Uparrow$
Gas processato CN $^{12}C$ $\Downarrow$ $^{14}N$ $\Uparrow$ $^{16}O$ $\Uparrow$
Gas processato CNO $ ^{12}C$ $\Downarrow$ $^{14}N$ $\Uparrow$ $^{16}O$ $\Downarrow$
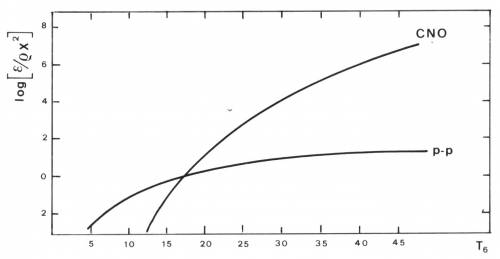
Fig. 4.9 La produzione di energia dalla catena pp e
dal ciclo CNO al variare della temperatura in milioni di gradi. Si
è assunta una composizione chimica solare.
La Figura 4.7 riporta l'andamento col tempo delle
abbondanze dei nuclei nel caso di combustione CNO in una miscela
con abbondanze originali solari alle condizioni indicate. Si nota
come prima $^{12}C$ e poi $^{16}O$ vengano trasformati in
$^{14}N$, mentre $^{13}C$ e $^{15}N$ vengono prodotti e mantenuti
all'equilibrio con i loro capostipiti $^{12}C$ e $^{14}N$. I tre
elementi più abbondanti del ciclo CNO risultano in ogni caso
$^{12}C$, $^{14}N$ e $^{16}O$, cui corrispondono le più piccole
sezioni d'urto per le reazioni di distruzione e, conseguentemente,
i tempi più lunghi per il raggiungimento dell'equilibrio. Per
seguire nel dattaglio l'evoluzione di una combustione CNO sarà
quindi sufficiente valutare istante per istante l'efficienza delle
tre reazioni
$^{12}$C + p $\rightarrow$ $^{13}$N + $\gamma$
$^{14}$N + p $\rightarrow$ $^{15}$O + $\gamma$
$^{16}$O + p $\rightarrow$ $^{17}$F + $\gamma$
e, eventualmente, se interessati ai dettagli temporali,
$^{13}$C + p $\rightarrow$ $^{14}$N + $\gamma$
che sono le quattro reazioni pseudoprimarie. Tutti gli altri
elementi possono essere riguardati come strettamente secondari,
raggiungendo in tempi trascurabili composizioni minime di
equilibrio. La Figura 4.8 mostra la dipendenza dalla
temperatura delle abbondanze di equilibrio dei quattro elementi
pseudoprimari.
L'efficienza della combustione CNO dipende per ogni temperatura
dalla abbondanza di tali elementi nel gas stellare. Nel caso di
gas con composizione solare ($Z\sim 0.02$) circa il 50\% della
massa degli elementi pesanti è attribuibile a C,N ed O e
attorno ai $17~ 10^6~ ∞K$ la combustione CNO inizia a predominare
sulla pp (Fig. 4.9). Tale soglia non dipende peraltro
criticamente dall'abbondanza di CNO. La dipendenza dalla
temperatura della generazione di energia va infatti nei due casi
come
$\varepsilon_{pp}\propto T^4 \ \ \varepsilon_{CNO}\propto T^{15}$
e modeste variazioni di temperatura sono quindi sufficienti per
bilanciare variazioni anche notevoli nell'abbondanza di nuclei
CNO.
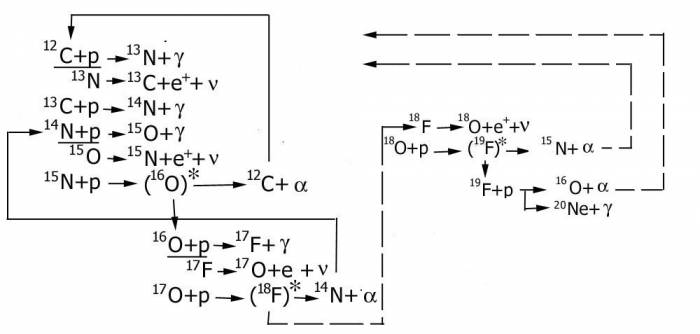
Fig. 4.10 Schema delle reazioni che compongono il
biciclo CN-NO. Sono indicate anche le reazioni che prendono
origine dai rari nuclei di $^{18}$F che decadono nel loro stato
fondamentale
La Figura 4.10 riporta uno schema delle reazioni che
compongono il biciclo CN-NO, con anche indicate le reazioni che
prendono origine dai rari nuclei di $^{18}$F che decadono nello
stato fondamentale anzichè restituire un nucleo di $^{14}$N ed
una particella $\alpha$. In linea di principio potrebbe
preoccupare l'esistenza al termine di queste ultime reazioni del
nucleo stabile $^{20}$Ne: ogni nucleo di $^{20}$Ne formato viene
infatti sottratto al ciclo, diminuendone l'efficienza. E' peraltro
facile verificare che il numero di nuclei di $^{20}$Ne così
prodotti risulta del tutto trascurabile. Dal rapporto delle
rispettive sezioni d'urto p,$\gamma$ e p,$\alpha$ si ricava
infatti la probabilità dei nuclei eccitati (= la frazione) di
decadere nel loro stato fondamentale per proseguire la catena di
reazioni. Risulta così
($^{18}$F)$^* \rightarrow ^{18}$F $\sim$ 0.3; ($^{19}$F)$^*
\rightarrow ^{19}$F $\sim$ 0.0008; ($^{20}$Ne)$^* \rightarrow
ricordando che circa solo l' 1% dei nuclei transita per il ciclo
NO si ricava che la probabilità di formare un nucleo di
$^{20}$Ne è minore di 10$^{-9}$. Questa probabilità va
confrontata con il numero di cicli che compie un nucleo prima che
sia esaurito l'idrogeno. Nel caso di materia di tipo solare,
Z=0.02, abbiamo indicato come vi sia all'incirca 1 nucleo di CNO
per ogni 1000 nuclei di idrogeno, e questo è quindi il numero di
cicli compiuto da ogni nucleo di CNO. E' subito visto che non solo
nel caso del Sole, ma anche per materia molto più povera di
metalli, la probabilità di formare $^{20}$Ne risulta
microscopica.
Per completare il quadro resta da indicare come la serie di reazioni sin qui descritta riposi sull'implicita assunzione che il tempo tra due successive catture protoniche sia lungo rispetto ai decadimenti $\beta$. Ciò è sempre vero nelle fasi di normale evoluzione delle strutture stellari, nelle quali la temperatura è governata dall'equilibrio idrostatico e le fusioni nucleari - come abbiamo indicato - sono eventi rari. Non è più vero durante le ultime fasi di implosione-esplosione, durante le quali la temperatura può aumentare improvvisamente di ordini di grandezza. In tal caso cresce la sezione d'urto per cattura protonica e diventa probabile che gli elementi del ciclo instabili $\beta^+$ catturino un protone prima di decadere. In tal caso si aprono ulteriori canali di combustione indicati con il termine CNO veloce ($\rightarrow $ A4.3).
